题目内容
13.设总体X~N(μ,σ 2),X1,X2,…,Xn是一个样本,$\overline{X}$,S2分别为样本均值和样本方差,试证:E[($\overline{X}$S2)2]=($\frac{{σ}^{2}}{n}$+μ2)(+$\frac{2{σ}^{4}}{n-1}$+σ4)分析 由相互独立事件性质得E[($\overline{X}$S2)2]=E(${\overline{X}}^{2}$)E[(S2)2]={D($\overline{X}$)+[E($\overline{X}$)2}{D(S2)+E[(S2)2]},由此利用X2分布的性质能证明E[($\overline{X}$S2)2]=($\frac{{σ}^{2}}{n}$+μ2)(+$\frac{2{σ}^{4}}{n-1}$+σ4).
解答 证明:∵$\overline{X}$,S2分别是正态总体N(μ,σ 2)的容量为n的样本均值和样本方差,
∴$\overline{X}$和S2相互独立,∴${\overline{X}}^{2}$与(S2)2也相互独立,
∴E[($\overline{X}$S2)2]=E(${\overline{X}}^{2}$)E[(S2)2]
={D($\overline{X}$)+[E($\overline{X}$)2}{D(S2)+E[(S2)2]},*
E($\overline{X}$)=μ,D($\overline{X}$)=$\frac{{σ}^{2}}{n}$,
由X2分布的性质得:E[$\frac{(n-1){S}^{2}}{{σ}^{2}}$]=n-1,D[$\frac{(n-1){S}^{2}}{{σ}^{2}}$]=2(n-1),
∴E(S2)=σ2,D(S2)=$\frac{2{σ}^{2}}{n-1}$,
将这些结果代入(*),得:
E[($\overline{X}$S2)2]=($\frac{{σ}^{2}}{n}$+μ2)(+$\frac{2{σ}^{4}}{n-1}$+σ4).
点评 本题考查正态分布的数学期望的相关公式的证明,是中档题,解题时要认真审题,注意X2分布的性质的合理运用.

| A. | d<a<c<b | B. | d<c<a<b | C. | a<d<b<c | D. | a<d<c<b |
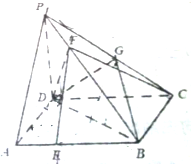 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC的中点,E,F分别为AB,PB上一点,AB=4$\sqrt{2}$,AE=$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC的中点,E,F分别为AB,PB上一点,AB=4$\sqrt{2}$,AE=$\sqrt{2}$,PB=4PF.