题目内容
已知函数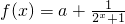 ,a∈R.
,a∈R.
(1)若函数f(x)是定义在R上的奇函数,求a的值;
(2)若函数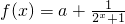 在区间(1,2)恰有一个零点,求实数a的取值范围.
在区间(1,2)恰有一个零点,求实数a的取值范围.
解:(1 )函数f(x)是定义在R上的奇函数有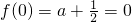
∴
(2)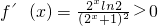 ∴f(x)是实数集R上的单调递增函数
∴f(x)是实数集R上的单调递增函数
又函数f(x)的图象不间断,在区间(1,2)恰有一个零点,有f(1)f(2)<0
即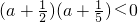 解之得
解之得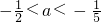 .
.
分析:(1)根据定义在R上的奇函数的图象必过原点,我们可以构造一个关于a的方程,解方程即可得到a的值;
(2)根据已知中函数的解析式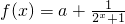 ,求出其导函数后,易判断f(x)是实数集R上的单调递增函数,则根据零点存在定理,我们可以将函数
,求出其导函数后,易判断f(x)是实数集R上的单调递增函数,则根据零点存在定理,我们可以将函数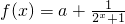 在区间(1,2)恰有一个零点,转化为一个关于a的不等式,解不等式即可求出实数a的取值范围.
在区间(1,2)恰有一个零点,转化为一个关于a的不等式,解不等式即可求出实数a的取值范围.
点评:本题考查的知识点是函数奇偶性的性质,及函数零点的判定定理,其中(1)的关键是奇函数的图象必要原点,(2)的关键是判断函数的单调性,进而将问题转化为一个不等式问题.
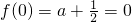
∴

(2)
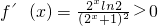 ∴f(x)是实数集R上的单调递增函数
∴f(x)是实数集R上的单调递增函数又函数f(x)的图象不间断,在区间(1,2)恰有一个零点,有f(1)f(2)<0
即
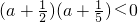 解之得
解之得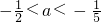 .
.分析:(1)根据定义在R上的奇函数的图象必过原点,我们可以构造一个关于a的方程,解方程即可得到a的值;
(2)根据已知中函数的解析式
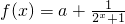 ,求出其导函数后,易判断f(x)是实数集R上的单调递增函数,则根据零点存在定理,我们可以将函数
,求出其导函数后,易判断f(x)是实数集R上的单调递增函数,则根据零点存在定理,我们可以将函数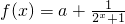 在区间(1,2)恰有一个零点,转化为一个关于a的不等式,解不等式即可求出实数a的取值范围.
在区间(1,2)恰有一个零点,转化为一个关于a的不等式,解不等式即可求出实数a的取值范围.点评:本题考查的知识点是函数奇偶性的性质,及函数零点的判定定理,其中(1)的关键是奇函数的图象必要原点,(2)的关键是判断函数的单调性,进而将问题转化为一个不等式问题.

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).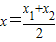 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.