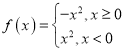题目内容
【题目】已知二次函数![]() 满足
满足![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在
在![]() 上单调,求
上单调,求![]() 的取值范围;
的取值范围;
(3)设![]() (
(![]() 且a≠1),(
且a≠1),(![]() 且
且![]() ),当
),当![]() 时,
时,![]() 有最大值14,试求a的值.
有最大值14,试求a的值.
【答案】(1)f(x)![]() ;(2)p≤﹣7,或者p≥﹣3;(3)a=3或
;(2)p≤﹣7,或者p≥﹣3;(3)a=3或![]()
【解析】
(1)利用![]() 代入化简得到答案.
代入化简得到答案.
(2)化简得到![]() ,得到对称轴
,得到对称轴![]() 或
或![]() 计算得到答案.
计算得到答案.
(3)![]() ,设
,设![]() 化简为二次函数计算得到答案.
化简为二次函数计算得到答案.
(1)∵f(x)=ax2+bx满足f(x﹣1)=f(x)+x﹣1,
∴a(x﹣1)2+b(x﹣1)=ax2+bx+x﹣1,即ax2﹣(2a﹣b)x+a﹣b=ax2+(b+1)x﹣1,
所以﹣(2a﹣b)=b+1,a﹣b=﹣1,得a![]() ,
,![]() ,
,
所以f(x)![]() .
.
(2)因为g(x)=﹣2f(x)+px=﹣2(![]() )+px=x2+(p﹣1)x,x∈[2,4]上单调,
)+px=x2+(p﹣1)x,x∈[2,4]上单调,
所以其对称轴x![]() 2,或者
2,或者![]() ,所以p≤﹣7,或者p≥﹣3.
,所以p≤﹣7,或者p≥﹣3.
(3)F(x)=4f(ax)+3a2x﹣1=a2x+2ax﹣1,(a>0且a≠1),
当x∈[﹣1,1]时,令t=ax,y=t2+2t﹣1=(t+1)2﹣2,
当a>1时,t![]() ,ymax=F(a)=(a+1)2﹣2=14,得a=3;
,ymax=F(a)=(a+1)2﹣2=14,得a=3;
当0<a<1时,t![]() ,
,![]() ,得a
,得a![]() .
.
故a=3或![]() .
.

【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(1)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(2)在上述样本中,学校从成绩为![]() 的学生中随机抽取
的学生中随机抽取![]() 人进行学习交流,求这
人进行学习交流,求这![]() 人来自同一个班级的概率.
人来自同一个班级的概率.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
【题目】某工厂生产一种产品,根据预测可知,该产品的产量平稳增长,记2015年为第1年,第x年与年产量![]() (万件)之间的关系如下表所示:
(万件)之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
| 4.00 | 5.52 | 7.00 | 8.49 |
现有三种函数模型:![]() ,
,![]() ,
,![]()
(1)找出你认为最适合的函数模型,并说明理由,然后选取![]() 这两年的数据求出相应的函数解析式;
这两年的数据求出相应的函数解析式;
(2)因受市场环境的影响,2020年的年产量估计要比预计减少30%,试根据所建立的函数模型,估计2020年的年产量.