题目内容
某校高一运动队为了备战校运动会需要购置一批运动鞋.已知该队伍有20名同学,统计表如下表.由于不小心弄脏了表格,有两个数据看不到:
下列说法正确的是( )
A.这组数据的中位数是40,众数是39. B.这组数据的中位数与众数一定相等.
C.这组数据的平均数P满足39<P<40. D.以上说法都不对.
| 鞋码 | 38 | 39 | 40 | 41 | 42 |
| 人数 | 5 | | | 3 | 2 |
A.这组数据的中位数是40,众数是39. B.这组数据的中位数与众数一定相等.
C.这组数据的平均数P满足39<P<40. D.以上说法都不对.
C
解:A、由于38、41、42码的数和为10,而39、40码对应的数不知,故不能确定出中位数和众数,故错误;
B、由于38、41、42码的数和为10,而39、40码对应的数不知,故不能确定出中位数和众数,也就不能确定出中位数与众数是否相等,故错误;
C、当39码的数为10,40码的数为0时,平均数=(38×5+39×10+41×3+42×2)÷20=39.35;
当39码的数为0,40码的数为10时,平均数=(38×5+40×10+41×3+42×2)÷20=39.85;
所以平均数不可能是39,故本选项错误;
D、当39码的数为10,40码的数为0时,平均数=(38×5+39×10+41×3+42×2)÷20=39.35;
当39码的数为0,40码的数为10时,平均数=(38×5+40×10+41×3+42×2)÷20=39.85;
∴这组数据的平均数故选C.
B、由于38、41、42码的数和为10,而39、40码对应的数不知,故不能确定出中位数和众数,也就不能确定出中位数与众数是否相等,故错误;
C、当39码的数为10,40码的数为0时,平均数=(38×5+39×10+41×3+42×2)÷20=39.35;
当39码的数为0,40码的数为10时,平均数=(38×5+40×10+41×3+42×2)÷20=39.85;
所以平均数不可能是39,故本选项错误;
D、当39码的数为10,40码的数为0时,平均数=(38×5+39×10+41×3+42×2)÷20=39.35;
当39码的数为0,40码的数为10时,平均数=(38×5+40×10+41×3+42×2)÷20=39.85;
∴这组数据的平均数故选C.

练习册系列答案
相关题目
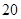 ~
~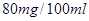 (不含80)之间,属于酒后驾车;在
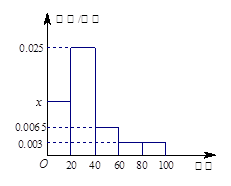
(不含80)之间,属于酒后驾车;在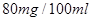 (含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:

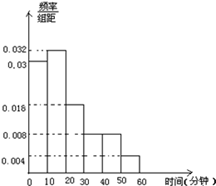


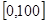 ,样本数据分组为
,样本数据分组为 ,
,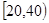 ,
,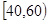 ,
,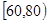 ,
,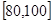 .
.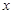 的值;
的值;