题目内容
有一个容量为100的样本,数据的分组及各组的频数如下:

(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图;(3)由直方图确定样本的中位数。


(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图;(3)由直方图确定样本的中位数。
解(1)样本的频率分布表;
频率折线图如图.
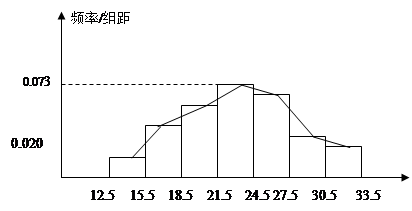
(3)由中位数两边矩形面积相等知,中位数为22.88
| 分组 | 频数 | 频率 |
 | 6 | 0.06 |
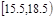 | 16 | 0.16 |
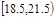 | 18 | 0.18 |
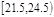 | 22 | 0.22 |
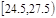 | 20 | 0.20 |
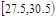 | 10 | 0.10 |
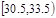 | 8 | 0.08 |
| 合计 | 100 | 1 |

(3)由中位数两边矩形面积相等知,中位数为22.88
解决总体分布估计问题的一般程序如下:
(1)先确定分组的组数(最大数据与最小数据之差除组距得组数);、(2)分别计算各组的频数及频率(频率=频率与组距的比值,乘以组距的长度)
(3)画出频率分布直方图,并作出相应的估计.
(1)由题中的所给数据,列成表格,即可得到频率分布表中的数据;、(2)由频率分布表中的数据,在横轴为数据,纵轴为 频率与组距的比值,,即可得到频率分布直方图;(3)为了确定样本的中位数,只须求出频率分步直方图中数据两侧等于0.5的频率即可.
解(1)样本的频率分布表;
频率折线图如图.

(3)由中位数两边矩形面积相等知,中位数为22.88
(1)先确定分组的组数(最大数据与最小数据之差除组距得组数);、(2)分别计算各组的频数及频率(频率=频率与组距的比值,乘以组距的长度)
(3)画出频率分布直方图,并作出相应的估计.
(1)由题中的所给数据,列成表格,即可得到频率分布表中的数据;、(2)由频率分布表中的数据,在横轴为数据,纵轴为 频率与组距的比值,,即可得到频率分布直方图;(3)为了确定样本的中位数,只须求出频率分步直方图中数据两侧等于0.5的频率即可.
解(1)样本的频率分布表;
| 分组 | 频数 | 频率 |
 | 6 | 0.06 |
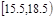 | 16 | 0.16 |
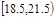 | 18 | 0.18 |
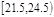 | 22 | 0.22 |
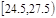 | 20 | 0.20 |
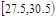 | 10 | 0.10 |
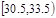 | 8 | 0.08 |
| 合计 | 100 | 1 |

(3)由中位数两边矩形面积相等知,中位数为22.88

练习册系列答案
相关题目
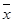 ,将10场比赛得分
,将10场比赛得分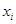 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的 大小为多少?并说明
大小为多少?并说明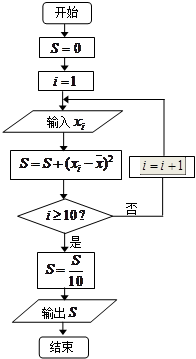
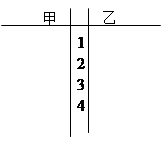
 .
.
 ,求
,求 ,
, ,
, 由此得到频率分布直方图如图,则这20名工人中一天生产该产品数量在
由此得到频率分布直方图如图,则这20名工人中一天生产该产品数量在 的人数是( )
的人数是( )


 ; (a,b精确到十分位)
; (a,b精确到十分位)
 间的频率是多少?
间的频率是多少?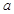
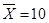 ,则该班成绩的方差
,则该班成绩的方差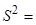 (精确到0.001)
(精确到0.001)