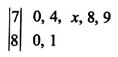题目内容
(本题满分12分)
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率直方图(如图),其中,上学所需时间的范围是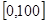 ,样本数据分组为
,样本数据分组为 ,
,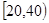 ,
,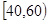 ,
,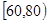 ,
,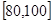 .
.
(Ⅰ)求直方图中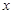 的值;
的值;
(Ⅱ)如果上学所需时间不小于1小时的学生中可以申请在学校住宿,请估计学校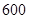
名新生中有多少名学生可以住宿.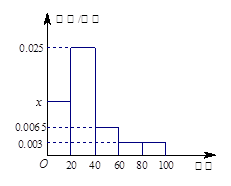
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率直方图(如图),其中,上学所需时间的范围是
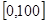 ,样本数据分组为
,样本数据分组为 ,
,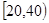 ,
,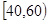 ,
,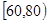 ,
,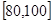 .
.(Ⅰ)求直方图中
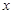 的值;
的值;(Ⅱ)如果上学所需时间不小于1小时的学生中可以申请在学校住宿,请估计学校
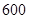
名新生中有多少名学生可以住宿.

(Ⅰ)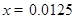 ;(Ⅱ)72
;(Ⅱ)72
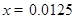 ;(Ⅱ)72
;(Ⅱ)72(I)由题意,可由直方图中各个小矩形的面积和为1求出x值.
(II)再求出小矩形的面积即上学所需时间不少于1小时组人数在样本中的频率,再乘以样本容量即可得到此组的人数即可.
解:(Ⅰ)由直方图可得:
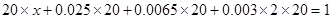 .
.
所以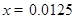 . ……………………(5分)
. ……………………(5分)
(Ⅱ)新生上学所需时间不少于1小时的频率为:
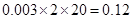 ,
,
因为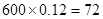 ,
,
所以600名新生中有72名学生可以申请住宿. .……………(12分)
(II)再求出小矩形的面积即上学所需时间不少于1小时组人数在样本中的频率,再乘以样本容量即可得到此组的人数即可.
解:(Ⅰ)由直方图可得:
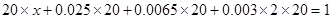 .
.所以
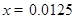 . ……………………(5分)
. ……………………(5分)(Ⅱ)新生上学所需时间不少于1小时的频率为:
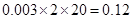 ,
, 因为
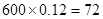 ,
,所以600名新生中有72名学生可以申请住宿. .……………(12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
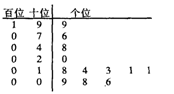
 名男志愿者和
名男志愿者和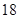 名女志愿者,调查发现,这
名女志愿者,调查发现,这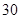 名志愿者的身高如下:(单位:cm )
名志愿者的身高如下:(单位:cm )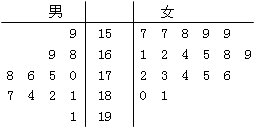
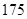 cm以上(包括
cm以上(包括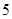 人,再从这
人,再从这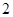 人,则至少有一人是“高个子”的概率是多少?
人,则至少有一人是“高个子”的概率是多少?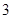 名志愿者,用
名志愿者,用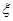 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出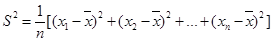 考虑,你认为哪位学生更稳定?请说明理由。
考虑,你认为哪位学生更稳定?请说明理由。