题目内容
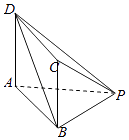
【题目】如图，直线 
平面 
，垂足为 
，正四面体(所有棱长都相等的三棱锥) 
的棱长为2， 
在平面 内， 
是直线 
上的动点，当 到 
的距离为最大时，正四面体在平面 上的射影面积为 ． 
【答案】
【解析】如下图所示，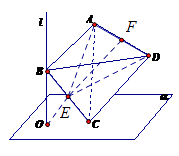
取 
中点 
， 
中点 
，连 
， 
， 
，易得 
为等腰三角形，∴ 
，而点 
是以 为直径的球面上的点，∴ 到 的距离为四面体上以 为直径的球面上的点到 的距离，故当 ， ， 三点共线时，最大距离 
，此时 
，故投影为以 为底边， 
为高的等腰三角形，∴ 
．
先确定直线BC与动点O的位置关系，得到最大距离是AD到球心的距离+半径，再考虑取得最大距离时四面体的投影情况，即可求得结论．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
