题目内容
用0,1,2,3,4,5这六个数字组成无重复数字的五位数.试分别求出符合下列条件的五位数的个数(最后结果用数字表达):
(1)总的个数;
(2)奇数;
(3)能被6整除的数;
(4)比12345大且能被5整除的数.
(1)总的个数;
(2)奇数;
(3)能被6整除的数;
(4)比12345大且能被5整除的数.
(1)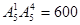 个 (3分)
个 (3分)
(2)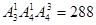 个 (6分)
个 (6分)
(3)末位为0有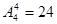 个,末位为2或4有
个,末位为2或4有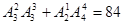 个,故共有108个.(10分)
个,故共有108个.(10分)
(4)末位为0有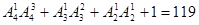 个,末位为5有
个,末位为5有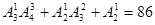 个,
个,
故共有205个.(14分)
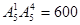 个 (3分)
个 (3分)(2)
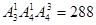 个 (6分)
个 (6分)(3)末位为0有
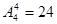 个,末位为2或4有
个,末位为2或4有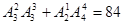 个,故共有108个.(10分)
个,故共有108个.(10分)(4)末位为0有
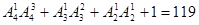 个,末位为5有
个,末位为5有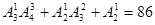 个,
个,故共有205个.(14分)
本题考查了排列与乘法原理的综合运用,对于特殊位置或者特殊元素应该特殊考虑,解题时要做到不重复不遗漏
解:(1)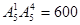 个;(2)
个;(2)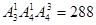 个;(3)108个;(4)205个.
个;(3)108个;(4)205个.
解:(1)
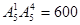 个;(2)
个;(2)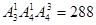 个;(3)108个;(4)205个.
个;(3)108个;(4)205个.
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
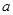 和
和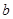 ,在直线
,在直线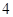 个点,直线
个点,直线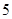 个点,以这些点为顶点作
个点,以这些点为顶点作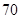 ;
;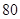 ;
; ;
;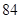
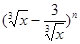 的展开式中,第6项为常数项。
的展开式中,第6项为常数项。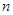 ;(2)求
;(2)求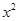 的项的系数;(3)求展开式中所有的有理项。
的项的系数;(3)求展开式中所有的有理项。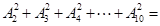 ___________(用数字作答);
___________(用数字作答);