题目内容
如图,PA⊥平面ABCD,ABCD为正方形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
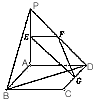
(1)求证:面EFG⊥面PAB;
(2)求异面直线EG与BD所成的角的余弦值;
(3)求点A到面EFG的距离。
| 解:建立如图所示的空间直角坐标系A-xyz, 则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0), P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0), (1)证明:∵ 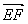 =(0,1,0), =(0,1,0), =(0,0,2), =(0,0,2),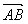 =(2,0,0), =(2,0,0),∴ 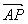 · ·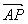 =0×0+1×0+0×2=0, =0×0+1×0+0×2=0,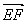 · ·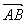 =0×2+1×0+0×0=0, =0×2+1×0+0×0=0,∴EF⊥AP,EF⊥AB, 又∵AP、AB 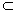 面PAB,且PA∩AB=A, 面PAB,且PA∩AB=A,∴EF⊥平面PAB, 又EF 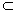 面EFG, 面EFG,∴平面EFG⊥平面PAB。 (2)∵ 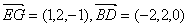 , ,∴ 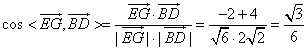 。 。(3)设平面EFC的法向量 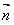 =(x,y,z), =(x,y,z), 则 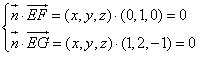 ,∴ ,∴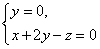 , ,令z=0,得 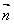 =(1,0,1), =(1,0,1),又 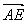 =(0,0,1), =(0,0,1),∴点A到平面EFG的距离 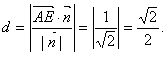 |

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点. 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2, (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.