Question

3．已知A（1，1），B（1，2），C（3，2），则△ABC内（包括边界）任意一点（x，y）满足的条件是$\left\{\begin{array}{l}{x≥1}\\{y≤2}\\{x-2y+1≤0}\end{array}\right.$．

Answer 1

分析 求出三角形三边满足的方程即可得到结论．

解答 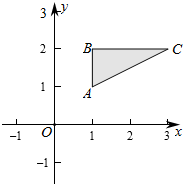解：∵A（1，1），B（1，2），C（3，2），
∴AB的方程为：x=1，
BC的方程为：y=2，
AC的方程为：$\frac{y-1}{2-1}=\frac{x-1}{3-1}$，
即x-2y+1=0，
则△ABC内（包括边界）任意一点（x，y）满足的条件是$\left\{\begin{array}{l}{x≥1}\\{y≤2}\\{x-2y+1≤0}\end{array}\right.$，
故答案为：$\left\{\begin{array}{l}{x≥1}\\{y≤2}\\{x-2y+1≤0}\end{array}\right.$

点评 本题主要考查二元一次不等式组与平面的关系，根据条件求出三角形三边对应的过程是解决本题的关键．