题目内容
11.已知三个数x,y,z满足$\frac{xy}{x+y}=-3,\frac{yz}{y+z}=\frac{4}{3},\frac{zx}{z+x}=-\frac{4}{3},\frac{xyz}{xy+yz+zx}$=-6.分析 $\frac{xy}{x+y}=-3$,$\frac{yz}{y+z}$=$\frac{4}{3}$,$\frac{zx}{z+x}$=$-\frac{4}{3}$,可得$\frac{1}{x}+\frac{1}{y}$=-$\frac{1}{3}$,$\frac{1}{y}+\frac{1}{z}$=$\frac{3}{4}$,$\frac{1}{x}+\frac{1}{z}$=-$\frac{3}{4}$,相加可得$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$=-$\frac{1}{6}$.代入即可得出.
解答 解:∵$\frac{xy}{x+y}=-3$,$\frac{yz}{y+z}$=$\frac{4}{3}$,$\frac{zx}{z+x}$=$-\frac{4}{3}$,
∴$\frac{1}{x}+\frac{1}{y}$=-$\frac{1}{3}$,$\frac{1}{y}+\frac{1}{z}$=$\frac{3}{4}$,$\frac{1}{x}+\frac{1}{z}$=-$\frac{3}{4}$,
联立解得$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$=-$\frac{1}{6}$.
∴$\frac{xyz}{xy+yz+xz}$=$\frac{1}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}$=-6.
故答案为:-6.
点评 本题考查了代数式的计算化简,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
6.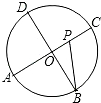 如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(单位:度),则下列图象中表示y与t之间函数关系最恰当的是( )
如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(单位:度),则下列图象中表示y与t之间函数关系最恰当的是( )
 如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(单位:度),则下列图象中表示y与t之间函数关系最恰当的是( )
如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(单位:度),则下列图象中表示y与t之间函数关系最恰当的是( )| A. | 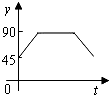 | B. | 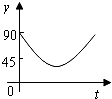 | C. |  | D. | 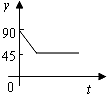 |
1.如图,在边长为e(e为自然对数的底数)的正方形中,阴影部分的面积为( )
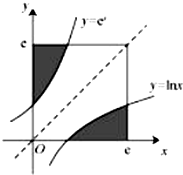

| A. | 2 | B. | $\frac{2}{e}$ | C. | e2 | D. | e |