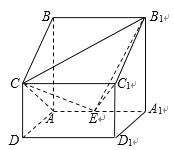
题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() ∥平面
∥平面![]() .
.
(Ⅲ)设![]() ,
,![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,确定点
?若存在,确定点![]() 的位置; 若不存在,说明理由.
的位置; 若不存在,说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)见解析; (Ⅲ)存在,![]() 为线段
为线段![]() 的中点,理由略.
的中点,理由略.
【解析】
试题分析:(Ⅰ)通过证得![]() ,且
,且![]() ,即可证得
,即可证得![]() 平面
平面![]() ,即证
,即证![]() ;
;
(Ⅱ) 设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,因为
,因为![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,由三角形的中位线定理得
的中点,由三角形的中位线定理得![]() ∥
∥![]() ,又由线面平行的判定定理即证
,又由线面平行的判定定理即证![]() ∥平面
∥平面![]() ;
;
(Ⅲ) 在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,且
,且![]() 为线段
为线段![]() 的中点.证明如下:由已知得
的中点.证明如下:由已知得![]() .
.
由已知![]() ,
,![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() ,可得
,可得![]() 平面
平面![]() .连接
.连接![]() .因为
.因为![]()
![]() 平面
平面![]() ,所以
,所以![]() ,易证
,易证![]() ,所以
,所以![]() 平面
平面![]() ,即可得
,即可得![]() .
.
试题解析:(Ⅰ)在三棱柱![]() 中,因为
中,因为![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,
所以![]() .
.
又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
而![]() ,
,
则![]() .
.
(Ⅱ)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,
,
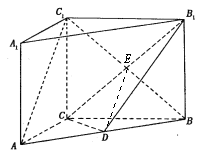
因为![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,
所以![]() ∥
∥![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
(Ⅲ)在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,且
,且![]() 为线段
为线段![]() 的中点.
的中点.
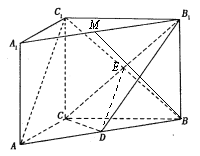
证明如下:因为![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,所以
,所以![]() .
.
由已知![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() .
.
取线段![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]()
![]() 平面
平面![]() ,所以
,所以![]() .
.
由已知![]() ,由平面几何知识可得
,由平面几何知识可得![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如表所示:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85(含85分)以上为优秀.有多少把握认为学生的数学成绩与物理成绩之间有关系( )
A.99.5%
B.99.9%
C.97.5%
D.95%