题目内容
已知偶函数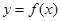 满足:当
满足:当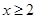 时,
时,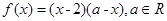 ,当
,当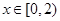 时,
时,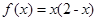 .
.
(Ⅰ).求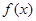 表达式;
表达式;
(Ⅱ).若直线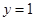 与函数
与函数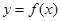 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数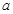 的取值范围;
的取值范围;
(Ⅲ).试讨论当实数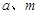 满足什么条件时,直线
满足什么条件时,直线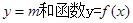 的图像恰有
的图像恰有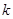 个公共点
个公共点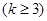 ,且这
,且这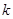 个公共点均匀分布在直线
个公共点均匀分布在直线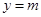 上.(不要求过程)
上.(不要求过程)
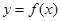 满足:当
满足:当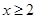 时,
时,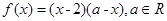 ,当
,当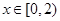 时,
时,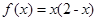 .
.(Ⅰ).求
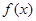 表达式;
表达式;(Ⅱ).若直线
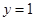 与函数
与函数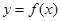 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数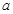 的取值范围;
的取值范围; (Ⅲ).试讨论当实数
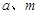 满足什么条件时,直线
满足什么条件时,直线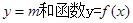 的图像恰有
的图像恰有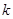 个公共点
个公共点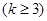 ,且这
,且这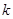 个公共点均匀分布在直线
个公共点均匀分布在直线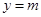 上.(不要求过程)
上.(不要求过程)(Ⅰ).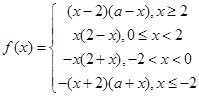 ;(Ⅱ).
;(Ⅱ).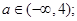 (Ⅲ).当
(Ⅲ).当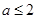 时,
时,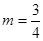 或
或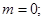
当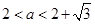 时,
时,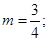 此时
此时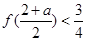 ; 当
; 当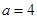 时,
时,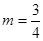 ,
,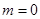 或
或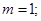
当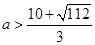 时
时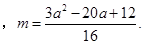 此时
此时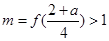 .
.
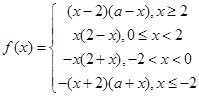 ;(Ⅱ).
;(Ⅱ).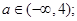 (Ⅲ).当
(Ⅲ).当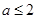 时,
时,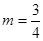 或
或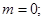
当
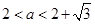 时,
时,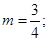 此时
此时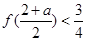 ; 当
; 当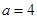 时,
时,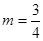 ,
,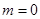 或
或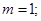
当
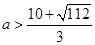 时
时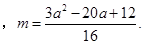 此时
此时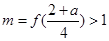 .
.试题分析:(1)由
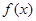 为偶函数,则有
为偶函数,则有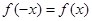 ,又因为当
,又因为当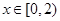 ,
,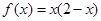 及
及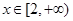 ,
,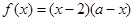 ,所以当
,所以当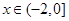 时,
时,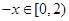 ,
,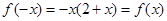 即可求出
即可求出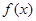 .当
.当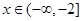 时,
时,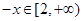 同理可求出此时的
同理可求出此时的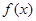 .(2)画出
.(2)画出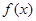 的大致图像,由图1易知,当
的大致图像,由图1易知,当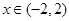 时,函数
时,函数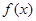 与
与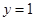 恰有两个交点,所以当
恰有两个交点,所以当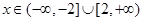 时,函数
时,函数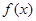 与
与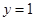 无交点,易得当
无交点,易得当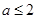 时恒成立,当
时恒成立,当 时,则有
时,则有 ,即可求出
,即可求出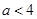 .
.当
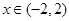 ,
,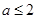 时,函数
时,函数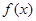 的图像如图2所示,此时直线
的图像如图2所示,此时直线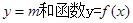 的图像若恰有
的图像若恰有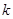 个公共点
个公共点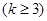 ,且这
,且这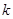 个公共点均匀分布在直线
个公共点均匀分布在直线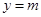 上,则易知
上,则易知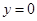 时符合题意,设
时符合题意,设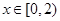 时由左到右的两个交点的横坐标分别为
时由左到右的两个交点的横坐标分别为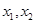 ,由函数的对称性易知,
,由函数的对称性易知,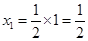 ,此时
,此时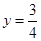 .其他情况同理即可求出.
.其他情况同理即可求出.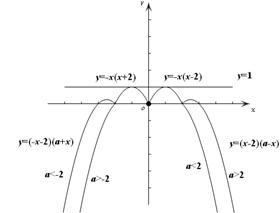
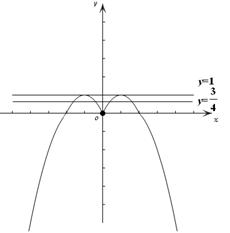
图1 图2
试题解析:(1)
 为偶函数,则有
为偶函数,则有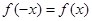
当
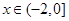 时,
时,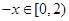 ,
,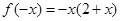 即
即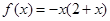
当
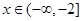 时,
时,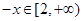 ,
,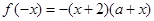 即
即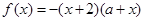
故有
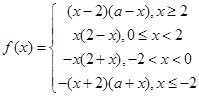
(2)如下图,当
 时,由图像易知函数
时,由图像易知函数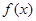 与
与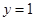 恰有两个交点
恰有两个交点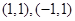
 当
当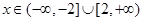 时,函数
时,函数 与
与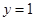 无交点
无交点由
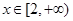 ,
,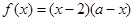
当
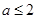 时,此时符合题意
时,此时符合题意当
 时,由
时,由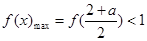 即
即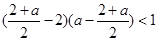
可得
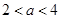
由偶函数的对称性可知
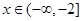 时,
时,与
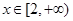 时的情况相同
时的情况相同故综上:
(3)当
 时,
时,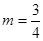 或
或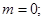
当
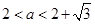 时,
时,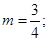 此时
此时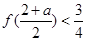
当
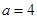 时,
时,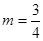 ,
,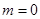 或
或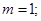
当
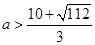 时
时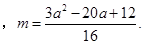 此时
此时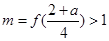

练习册系列答案
相关题目
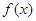 的图象形如字母M,奇函数
的图象形如字母M,奇函数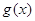 的图象形如字母N,若方程:
的图象形如字母N,若方程: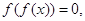
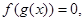
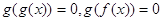 的实数根的个数分别为a、b、c、d,则
的实数根的个数分别为a、b、c、d,则 =( )
=( ) 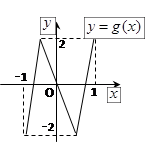
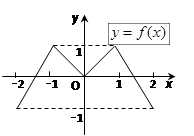
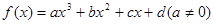 的对称中心为
的对称中心为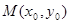 ,记函数
,记函数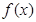 的导函数为
的导函数为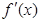 ,
,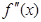 ,则有
,则有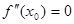 .若函数
.若函数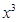 –
–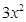 ,则可求得
,则可求得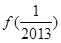 +
+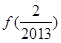 +
+
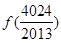 +
+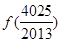 =( )
=( )
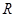 上的偶函数
上的偶函数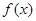 满足
满足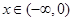 时,
时,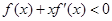 成立,若
成立,若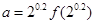 ,
,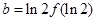 ,
,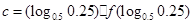 ,则
,则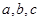 的大小关系是( )
的大小关系是( )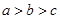
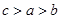
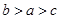
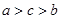
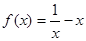 ,
,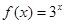 ,
,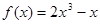 ,
,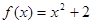 中,奇函数的个数是 ( )
中,奇函数的个数是 ( ) 上的奇函数
上的奇函数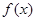 满足
满足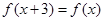 ,当
,当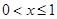 时,
时,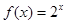 ,则
,则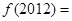 ( )
( )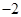
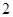
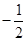
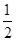
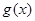 是定义在R上以1为周期的函数,若
是定义在R上以1为周期的函数,若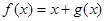 在区间
在区间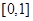 上的值域为
上的值域为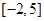 ,则
,则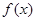 在区间
在区间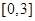 上的值域为_____.
上的值域为_____.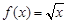
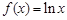
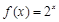
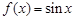
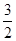 )与b=f(
)与b=f(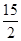 )的大小关系为____________.
)的大小关系为____________.