题目内容
函数f(x)=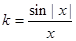 (k>0)有且仅有两个不同的零点
(k>0)有且仅有两个不同的零点 ,
, (
( >
> ),则以下有关两零点关系的结论正确的是
),则以下有关两零点关系的结论正确的是
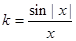 (k>0)有且仅有两个不同的零点
(k>0)有且仅有两个不同的零点 ,
,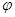 (
( >
>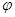 ),则以下有关两零点关系的结论正确的是
),则以下有关两零点关系的结论正确的是A.sin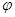 = =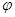 cos cos | B.sin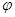 =- =-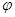 cos cos |
C.sin = = cos cos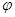 | D.sin =- =- cos cos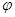 |
D
解:依题意可知x>0(x不能等于0)
令y1=|sinx|,y2=kx,然后分别做出两个函数的图象.
因为原方程有且只有两个解,所以y2与y1仅有两个交点,而且第二个交点是y1和y2相切的点,
即点(θ,|sinθ|)为切点,因为(-sinθ)′=-cosθ,所以切线的斜率k=-cosθ.而且点(φ,sinφ)在切线y2=kx=-cosθx上.
于是将点(φ,sinφ)代入切线方程y2=xcosθ可得:sin =-
=- cos
cos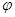 .
.
故选D
令y1=|sinx|,y2=kx,然后分别做出两个函数的图象.
因为原方程有且只有两个解,所以y2与y1仅有两个交点,而且第二个交点是y1和y2相切的点,
即点(θ,|sinθ|)为切点,因为(-sinθ)′=-cosθ,所以切线的斜率k=-cosθ.而且点(φ,sinφ)在切线y2=kx=-cosθx上.
于是将点(φ,sinφ)代入切线方程y2=xcosθ可得:sin
 =-
=- cos
cos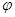 .
.故选D

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
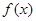 的定义域为
的定义域为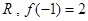 ,对任意
,对任意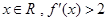 ,则
,则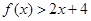 的解集为( )
的解集为( )
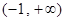
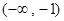
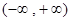
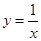 在点
在点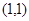 处的切线与直线
处的切线与直线 垂直,则
垂直,则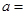 .
. 是曲线
是曲线 上的一点,若曲线在
上的一点,若曲线在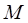 处的切线的倾斜角是均不小于
处的切线的倾斜角是均不小于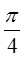 的锐角,则实数
的锐角,则实数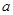 的取值范围是( )
的取值范围是( )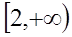

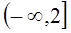
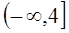
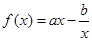 ,曲线
,曲线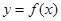 在点
在点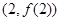 处的切线方程为
处的切线方程为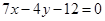 .
.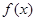 的解析式;(2)证明:曲线
的解析式;(2)证明:曲线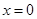 和直线
和直线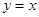 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.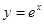 的切线,则切点坐标是________,切线斜率是_______.
的切线,则切点坐标是________,切线斜率是_______.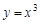 在点
在点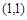 处的切线方程是 ;
处的切线方程是 ; 为曲线
为曲线 与
与 的公共点,且两条曲线在点
的公共点,且两条曲线在点 = .
= . 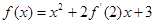 ,则
,则 .
.