题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)在(1)的条件下,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)单调递增区间为![]() ,
,![]() ;单调递减区间为
;单调递减区间为![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)将![]() 代入函数
代入函数![]() 中,求出导函数大于零求出递增区间,导函数小于零求出递减区间;(2)分为
中,求出导函数大于零求出递增区间,导函数小于零求出递减区间;(2)分为![]() 和
和![]() 和
和![]() 三种情况分别判断
三种情况分别判断![]() 在
在![]() 上的单调性,然后求出最大值和最小值.
上的单调性,然后求出最大值和最小值.
(1)若![]() ,则
,则![]() ,求导得
,求导得![]() .
.
因为![]() ,令
,令![]() ,即
,即![]() ,
,
解得![]() 或
或![]()
令![]() ,即
,即![]() ,解得
,解得![]()
∴函数![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减.
上递减.
即函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ;单调递减区间为
;单调递减区间为![]()
(2)①当![]() 时,∵
时,∵![]() 在
在![]() 上递减,
上递减,
∴![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
②当![]() 时,
时,
∵![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增,且
上递增,且![]() ,
,
∴![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
③当![]() 时,
时,
∵![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增,且
上递增,且![]() ,
,
∴![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案【题目】20名高二学生某次数学考试成绩(单位:分)的频率分布直方图如图:
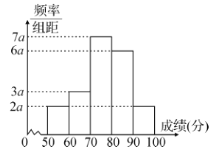
(1)求频率分布直方图中![]() 的值;
的值;
(2)分别求出成绩落在![]() 与
与![]() 中的学生人数;
中的学生人数;
(3)从成绩在![]() 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在![]() 中的概率.
中的概率.
【题目】某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格.据统计,高一年级女生需要不同规格校服的频数如表所示.
校服规格 | 155 | 160 | 165 | 170 | 175 | 合计 |
频数 | 39 | 64 | 167 | 90 | 26 | 386 |
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论用表中的数据估计全国高一年级女生校服规格的合理性.
【题目】某单位有2000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
老年 | 40 | 40 | 40 | 80 | 200 |
中年 | 80 | 120 | 160 | 240 | 600 |
青年 | 40 | 160 | 280 | 720 | 1 200 |
小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人调查身体状况,则应怎样抽样?
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
