题目内容
已知△ABC的面积S满足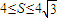 ,且
,且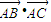 =-8.
=-8.(Ⅰ)求角A的取值范围;
(Ⅱ)若函数
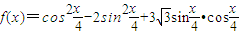 ,求f(A)的最大值.
,求f(A)的最大值.
【答案】分析:(Ⅰ)利用两个向量的数量积的定义求出 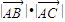 =
=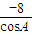 ,再由
,再由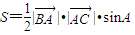 ,可得
,可得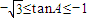 ,根据A为三角形的内角,求出
,根据A为三角形的内角,求出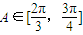 .
.
(Ⅱ)利用,二倍角公式及两角和的正弦公式化简f(A)的解析式为 ,可得当
,可得当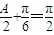 时,f(A)取得最大值
时,f(A)取得最大值 .
.
解答:解:(Ⅰ)∵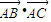 =-8,∴
=-8,∴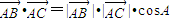 =-8,∴
=-8,∴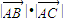 =
=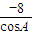 ①.
①.
∵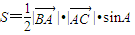 ②,将①代入②得S=-4tanA,由
②,将①代入②得S=-4tanA,由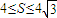 ,得
,得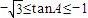 ,
,
又A∈(0,π),∴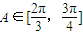 .
.
(Ⅱ)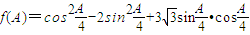 =
=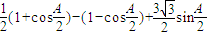 =
=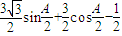
=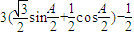 =
=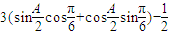 =
=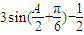 ,
,
当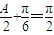 ,即A=
,即A= 时,
时,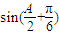 取得最大值,同时,f(A)取得最大值
取得最大值,同时,f(A)取得最大值 .
.
点评:本题主要考查两个向量的数量积的定义,二倍角公式的应用,两角和的正弦公式,正弦函数的定义域和值域,化简f(A)的解析式,是解题的关键.
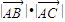 =
=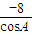 ,再由
,再由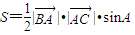 ,可得
,可得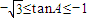 ,根据A为三角形的内角,求出
,根据A为三角形的内角,求出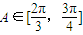 .
.(Ⅱ)利用,二倍角公式及两角和的正弦公式化简f(A)的解析式为
 ,可得当
,可得当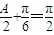 时,f(A)取得最大值
时,f(A)取得最大值 .
.解答:解:(Ⅰ)∵
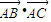 =-8,∴
=-8,∴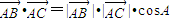 =-8,∴
=-8,∴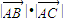 =
=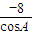 ①.
①.∵
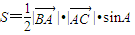 ②,将①代入②得S=-4tanA,由
②,将①代入②得S=-4tanA,由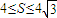 ,得
,得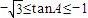 ,
,又A∈(0,π),∴
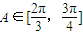 .
.(Ⅱ)
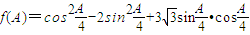 =
=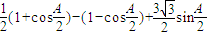 =
=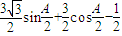
=
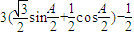 =
=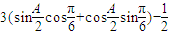 =
=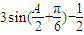 ,
,当
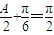 ,即A=
,即A= 时,
时,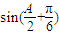 取得最大值,同时,f(A)取得最大值
取得最大值,同时,f(A)取得最大值 .
.点评:本题主要考查两个向量的数量积的定义,二倍角公式的应用,两角和的正弦公式,正弦函数的定义域和值域,化简f(A)的解析式,是解题的关键.

练习册系列答案
相关题目