题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )的右顶点为
)的右顶点为![]() .左、右焦点分别为
.左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线交椭圆于点
轴的直线交椭圆于点![]() (
(![]() 在第象限),直线
在第象限),直线![]() 的斜率为
的斜率为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不与
不与![]() 、
、![]() 重合),若
重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】
(1)根据条件建立方程组进行求解;
(2)先验证设直线![]() 的斜率不存在时是否符合题意,再设直线
的斜率不存在时是否符合题意,再设直线![]() 的斜率为
的斜率为![]() ,联立方程组,根与系数的关系 ,结合
,联立方程组,根与系数的关系 ,结合![]() ,可将
,可将![]() (或
(或![]() 的坐标用
的坐标用![]() 表示,再利用点
表示,再利用点![]() 在椭圆
在椭圆![]() 上,求得
上,求得![]() ,从而求得
,从而求得![]() 的方程.
的方程.
解:(1)![]() ,
,![]() ,由题意得
,由题意得
解得![]() ,
,![]()
因此椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由![]() 得
得![]() ,即
,即![]()
若直线![]() 的斜率不存在,则
的斜率不存在,则![]() ,
,![]() ,不满足
,不满足![]()
因此直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,
,
由 ,得
,得![]()
![]() 恒成立
恒成立
设![]() ,
,![]() ,则
,则![]()
由![]() ,
,![]() ,
,![]() 得
得
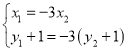 ,从而
,从而
即
代入椭圆方程,得
解得![]() ,即
,即![]()
因此直线![]() 的方程为
的方程为![]() ,即
,即![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为了研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组: ![]() ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.

(1)根据“25周岁以上组”的频率分布直方图,求25周岁以上组工人日平均生产件数的中位数的估计值(四舍五入保留整数);
(2)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(3)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“生产能手与工人所在年龄组有关”?
的把握认为“生产能手与工人所在年龄组有关”?
生产能手 | 非生产能手 | 合计 | |
25周岁以上组 | |||
25周岁以下组 | |||
合计 |
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
附: