题目内容
2.已知向量$\overrightarrow{OA},\overrightarrow{OB}$满足$\overrightarrow{|{OA}|}=\overrightarrow{|{OB}|}=1,\overrightarrow{OA}⊥\overrightarrow{OB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}({λ,μ∈R})$,若M为AB的中点,并且$|{\overrightarrow{MC}}|=1$,则λ+μ的最大值是( )| A. | $1-\sqrt{3}$ | B. | $1+\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $1+\sqrt{3}$ |
分析 向量$\overrightarrow{OA},\overrightarrow{OB}$满足$|\overrightarrow{OA}|=|\overrightarrow{OB}|$=1,$\overrightarrow{OA}⊥\overrightarrow{OB}$,不妨取A(1,0),B(0,1).利用中点坐标公式可得M$(\frac{1}{2},\frac{1}{2})$.由$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$=(λ,μ).及其$|{\overrightarrow{MC}}|=1$,可得$(λ-\frac{1}{2})^{2}+(μ-\frac{1}{2})^{2}$=1,换元$λ=\frac{1}{2}+cosθ$,μ=$\frac{1}{2}$+sinθ,θ∈[0,2π).即可得出.
解答 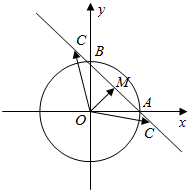 解:如图所示,
解:如图所示,
∵向量$\overrightarrow{OA},\overrightarrow{OB}$满足$|\overrightarrow{OA}|=|\overrightarrow{OB}|$=1,$\overrightarrow{OA}⊥\overrightarrow{OB}$,
不妨取A(1,0),B(0,1).
∵M为AB的中点,
∴M$(\frac{1}{2},\frac{1}{2})$.
∵$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$=λ(1,0)+μ(0,1)=(λ,μ).
∵$|{\overrightarrow{MC}}|=1$,
∴$(λ-\frac{1}{2})^{2}+(μ-\frac{1}{2})^{2}$=1,
设$λ=\frac{1}{2}+cosθ$,μ=$\frac{1}{2}$+sinθ,θ∈[0,2π).
则λ+μ=1+sinθ+cosθ=1+$\sqrt{2}sin(θ+\frac{π}{4})$$≤1+\sqrt{2}$,当$sin(θ+\frac{π}{4})$=1时取等号.
∴λ+μ的最大值是1+$\sqrt{2}$.
故选:B.
点评 本题考查了向量的运算及其模的计算公式、圆的标准方程、三角函数换元方法,考查了推理能力与计算能力,属于中档题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | m>2 | B. | m<2 | C. | m<0或m>2 | D. | 0<m<2 |
 已知,正方形ABCD-A1B1C1D1,E、M、F分别是AD、CD、CC1的中点,
已知,正方形ABCD-A1B1C1D1,E、M、F分别是AD、CD、CC1的中点,