题目内容
已知甲箱中只放有x个红球与y个白球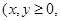 且
且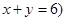 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
(Ⅰ)记取出的3个球的颜色全不相同的概率为P,求当P取得最大值时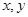 的值;
的值;
(Ⅱ)当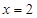 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数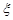 的期望
的期望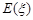 .
.
(I) 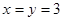 .
.
(II)红球个数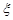 的分布列为
的分布列为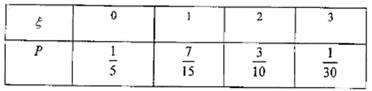
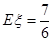 .
.
解析试题分析:(I)由题意知 ,
,
当且仅当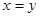 时等号成立,所以,当
时等号成立,所以,当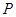 取得最大值时
取得最大值时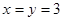 .
.
(II)当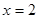 时,即甲箱中有
时,即甲箱中有 个红球与
个红球与 个白球,所以
个白球,所以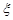 的所有可能取值为
的所有可能取值为
则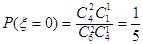 ,
,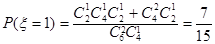 ,
,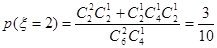 ,
,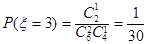 ,
,
所以红球个数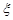 的分布列为
的分布列为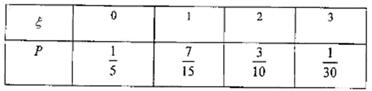
于是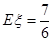 .
.
考点:本题主要考查独立事件的概率计算,随机变量分布列及其数学期望,均值定理的应用。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。独立事件的概率的计算问题,关键是明确事件、用好公式。本题综合性较强,特别是与不等式相结合,有新意。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛. 该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 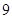 |  |
| [70,80) | 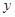 |  |
| [80,90) | 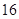 | 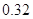 |
| [90,100) |  |  |
| 合 计 | 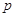 |  |
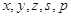 的值;
的值;(Ⅱ)按规定,预赛成绩不低于
 分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一·二班在决赛中进入前三名的人数为
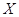 ,求
,求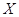 的分布列和数学期望.
的分布列和数学期望. 在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙,情况如下表:
| | 科目甲 | 科目乙 | 总计 |
| 第一小组 | 1 | 5 | 6 |
| 第二小组 | 2 | 4 | 6 |
| 总计 | 3 | 9 | 12 |
(1)求选出的4 人均选科目乙的概率;
(2)设
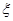 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求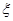 的分布列和数学期望.
的分布列和数学期望. 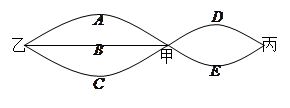
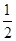 、
、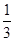 、
、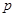 ,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为 .
.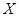 ,求
,求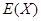 .
.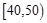 ,
,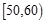 ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.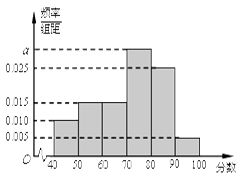
 的值
的值 ,其中:
,其中: ,记函数
,记函数 满足条件:
满足条件: 的事件为A,求事件A发生的概率。
的事件为A,求事件A发生的概率。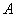 、
、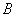 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是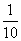 ,
, 、
、 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
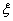 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求 ,不堵车的概率为
,不堵车的概率为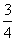 ;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.
;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.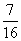 ,求走二号公路堵车的概率;
,求走二号公路堵车的概率;