题目内容
若数列{an}满足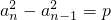 (p为常数,n≥2,n∈N*),则称数列{an}为等方差数列,p为公方差,已知正数等方差数列{an}的首项a1=1,且a1,a2,a5成等比数列,a1≠a2,设集合
(p为常数,n≥2,n∈N*),则称数列{an}为等方差数列,p为公方差,已知正数等方差数列{an}的首项a1=1,且a1,a2,a5成等比数列,a1≠a2,设集合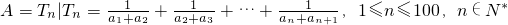 ,取A的非空子集B,若B的元素都是整数,则B为“完美子集”,那么集合A中的完美子集的个数为
,取A的非空子集B,若B的元素都是整数,则B为“完美子集”,那么集合A中的完美子集的个数为
- A.64
- B.63
- C.32
- D.31
B
分析:根据正数等方差数列{an}的首项a1=1,且a1,a2,a5成等比数列,a1≠a2,确定数列的通项,利用裂项法求和,可得A中的整数元素为1,2,3,4,5,6,即可求得结论.
解答:设数列{an}为正数等方差数列,p为公方差,则
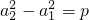 ,
,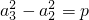 ,
,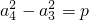 ,
,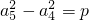
∴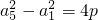
∵a1=1,∴a2=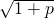 ,a5=
,a5=
∵a1,a2,a5成等比数列,
∴1+p=
∴p=0或p=2
∵a1≠a2,∴p=2
∴an=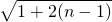 =
=
∴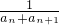 =
=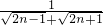 =
= (
( -
- )
)
∴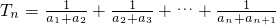 =
= (
( -1)
-1)
∴A中的整数元素为1,2,3,4,5,6
∵A的非空子集B,若B的元素都是整数,
∴集合A中的完美子集的个数为26-1=63
故选B.
点评:本题考查新定义,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.
分析:根据正数等方差数列{an}的首项a1=1,且a1,a2,a5成等比数列,a1≠a2,确定数列的通项,利用裂项法求和,可得A中的整数元素为1,2,3,4,5,6,即可求得结论.
解答:设数列{an}为正数等方差数列,p为公方差,则
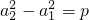 ,
,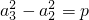 ,
,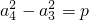 ,
,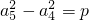
∴
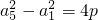
∵a1=1,∴a2=
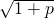 ,a5=
,a5=
∵a1,a2,a5成等比数列,
∴1+p=

∴p=0或p=2
∵a1≠a2,∴p=2
∴an=
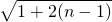 =
=
∴
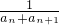 =
=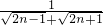 =
= (
( -
- )
)∴
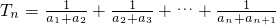 =
= (
( -1)
-1)∴A中的整数元素为1,2,3,4,5,6
∵A的非空子集B,若B的元素都是整数,
∴集合A中的完美子集的个数为26-1=63
故选B.
点评:本题考查新定义,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目