题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=4,DC=3,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=4,DC=3,E是PC的中点.(I)证明:PA∥平面BDE;
(II)求△PAD以PA为轴旋转所围成的几何体体积.
分析:(I)连接AC交BD于O,连接EO.在△PCA中,根据中位线定理得到OE∥PA.再结合直线与平面平行的判定定理,可证出PA∥平面BDE.
(II)过D作PA的垂线,垂足为H,则△PAD以PA为轴旋转所围成的几何体为DH为半径,分别以PH,AH为高的两个圆锥的组合体.利用锥体的体积计算公式,结合题中条件不难求出DH的长,从而算出该几何体的体积.
(II)过D作PA的垂线,垂足为H,则△PAD以PA为轴旋转所围成的几何体为DH为半径,分别以PH,AH为高的两个圆锥的组合体.利用锥体的体积计算公式,结合题中条件不难求出DH的长,从而算出该几何体的体积.
解答:解:(I)连接AC交BD于O,连接EO.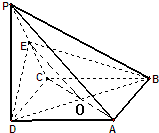
∵ABCD是正方形,∴O为AC中点,
∵E为PA的中点,∴OE∥PA.
又∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE.
(II)过D作PA的垂线,垂足为H,则
△PAD以以PA为轴旋转所围成的几何体为DH为半径,分别以PH,AH为高的两个圆锥的组合体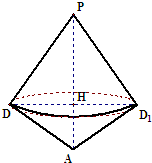
∵侧棱PD⊥底面ABCD,AD⊆底面ABCD
∴PD⊥AD,
∵PD=4,DA=DC=3,∴PA=5,DH=
=
=
所以,该几何体的体积为:V=
πDH2•PH+
πDH2•AH
=
πDH2•PA=
π×(
)2×5=
π.

∵ABCD是正方形,∴O为AC中点,
∵E为PA的中点,∴OE∥PA.
又∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE.
(II)过D作PA的垂线,垂足为H,则
△PAD以以PA为轴旋转所围成的几何体为DH为半径,分别以PH,AH为高的两个圆锥的组合体

∵侧棱PD⊥底面ABCD,AD⊆底面ABCD
∴PD⊥AD,
∵PD=4,DA=DC=3,∴PA=5,DH=
| PD•DA |
| PA |
| 4×3 |
| 5 |
| 12 |
| 5 |
所以,该几何体的体积为:V=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 3 |
| 12 |
| 5 |
| 48 |
| 5 |
点评:本题给出特殊四棱锥,求证线面平行并且求旋转体的体积,着重考查了线面平行的判定、线面垂直的性质和棱锥的体积公式等知识,属于基础题.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.