题目内容
如右图是某几何体的三视图,则此几何体的体积是( )
| A.36 | B.108 | C.72 | D.180 |
B
解析试题分析:由三视图可知该几何体是如图所示的图形: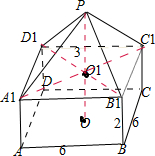
上面是一个正四棱锥,其底面是边长为6的正方形,高为3;下面是一个长方体,三条棱长分别为6,6,2.∴V体积=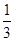 ×62×3+6×6×2=108.故选B.
×62×3+6×6×2=108.故选B.
考点:本题考查了三视图的运用
点评:由三视图正确恢复原几何体是解决问题的关键

练习册系列答案
相关题目
将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括
| A.一个圆台、两个圆锥 | B.两个圆台、一个圆柱 |
| C.两个圆台、一个圆锥 | D.一个圆柱、两个圆锥 |
一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )
| A.球 | B.三棱锥 | C.正方体 | D.圆柱 |
在一个几何体的三视图中,正视图和俯视图如下图所示,则该几何体的体积为( ) 
A. cm3( cm3( | B. cm3 cm3 | C. cm3 cm3 | D. cm3 cm3 |
半径为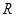 的半圆卷成一个圆锥,则它的体积为( ).
的半圆卷成一个圆锥,则它的体积为( ).
A.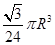 | B. | C. | D. |
已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则 ”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若
”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体ABCD中,若 的中心为M,四面体内部一点O到四面体各面的距离都相等”,则
的中心为M,四面体内部一点O到四面体各面的距离都相等”,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
若某多面体的三视图如图所示,则此多面体的体积是( )
| A.2 | B.4 | C.6 | D.12 |





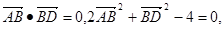 若将其沿BD折起,使平面ABD
若将其沿BD折起,使平面ABD 平面BDC则三棱锥A-BCD的外接球的表面积为:( )
平面BDC则三棱锥A-BCD的外接球的表面积为:( )