Question

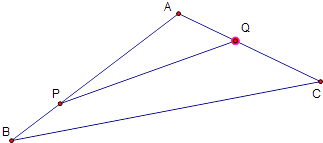
【题目】如图，将一副三角板拼接，使它们有公共边BC，且使两个三角形所在的平面互相垂直，若

∠BAC＝90°，AB＝AC，∠CBD＝90°，∠BDC＝60°，BC＝6。

⑴ 求证：平面平面ACD；

⑵ 求二面角的平面角的正切值；

⑶ 设过直线AD且与BC平行的平面为，求点B到平面的距离。

Answer 1

【答案】（1）见解析；（2）2；（3）

【解析】分析：（1）要证平面平面ACD，关键是证AC⊥平面ABD，只需证AC⊥BD，AC⊥AB，利用平面BCD⊥平面ABC，BD⊥BC即可；

（2）设BC中点为E，连接AE，过E作EF⊥CD于F，连接AF，由三垂线定理，可得∠EFA为二面角的平面角，从而可求；

（3）过点D作DG//BC，且CB＝DG，连接AG，利用等体积法即可.

详解：⑴平面BCD⊥平面ABC，BD⊥BC，平面BCD∩平面ABC＝BC，

∴BD⊥平面ABC.

AC平面ABC，

∴AC⊥BD，

又AC⊥AB，BD∩AB＝B，

∴AC⊥平面ABD.

又AC平面ACD，

∴平面ABD⊥平面ACD；

⑵设BC中点为E，连AE，过E作EF⊥CD于F，连接AF，

由三垂线定理：∠EFA为二面角的平面角.

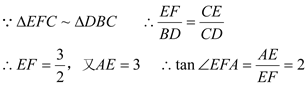
∴二面角的平面角的正切值为2.

（3）过点D作DG//BC，且CB＝DG，连接AG

∥平面ADG，

∴B到平面ADG的距离等于C到平面ADG的距离h

.