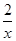题目内容
设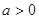 且
且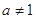 ,函数
,函数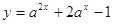 在
在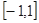 的最大值是14,求
的最大值是14,求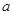 的值。
的值。
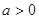 且
且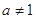 ,函数
,函数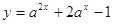 在
在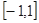 的最大值是14,求
的最大值是14,求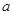 的值。
的值。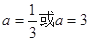
试题分析:先利用分类讨论思想对a分类
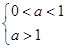 再利用换元法将y变成
再利用换元法将y变成 ,然后利用二次函数对称轴t=-1,所以在区间t
,然后利用二次函数对称轴t=-1,所以在区间t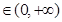 上函数单调递增,即可确定f(x)max=
上函数单调递增,即可确定f(x)max=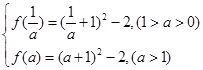 由题得f(x)max=14,所以可以求出
由题得f(x)max=14,所以可以求出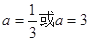 .
.试题解析:令
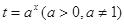 ,则原函数化为
,则原函数化为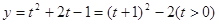 2分
2分①当
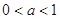 时,
时,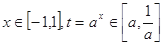 3分
3分此时
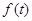 在
在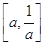 上为增函数,所以
上为增函数,所以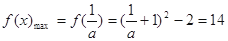 6分
6分所以
 7分
7分②当
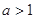 时,
时,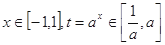 8分
8分此时
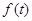 在
在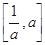 上为增函数,所以
上为增函数,所以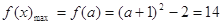 10分
10分所以
 11分
11分综上
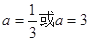 12分
12分
练习册系列答案
相关题目
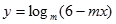 在
在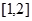 上单调递减.
上单调递减.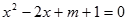 在
在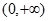 内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.
内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.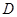 的函数
的函数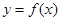 ,若同时满足:
,若同时满足: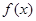 在
在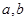 ]
]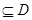 ,使
,使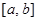 上的值域为
上的值域为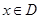 )叫做闭函数.
)叫做闭函数.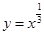 符合条件②的区间
符合条件②的区间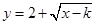 是闭函数,求实数
是闭函数,求实数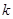 的取值范围.
的取值范围.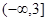 上
上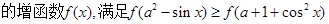 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。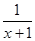
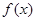 是定义在R上的偶函数,且在区间[0,+∞)上单调递增,则满足不等式
是定义在R上的偶函数,且在区间[0,+∞)上单调递增,则满足不等式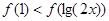 的
的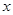 的取值范围是 .
的取值范围是 .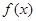 在区间
在区间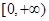 单调递增,则满足
单调递增,则满足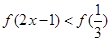 的x取值范围是( )
的x取值范围是( )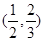
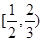
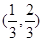


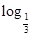 |x|
|x|