题目内容
已知f(x)是定义在R上的不恒为零的函数,且对于任意实数a、b∈R满足:f(a·b)=af(b)+bf(a),f(2)=2,an=![]() (n∈N*),bn=
(n∈N*),bn=![]() (n∈N*),考查下列结论
(n∈N*),考查下列结论
①f(0)=f(1); ②f(x)是偶函数;
③数列{an}为等比数列; ④数列{bn}为等差数列.
其中正确的结论是 ( )
A.①②③ B.①③④ C.①②④ D.①③
答案:B 【解析】分别考查各选项;①由f(a·b)=af(b)+bf(a),分别赋值令a=b=0得f(0)=0,a=b=1,得f(1)=0,故结论正确,(实质上由各选项都含有①可知该命题必正确)③由f(2)=2得f(22)=f(2·2)=4f(2)=8,f(23)=f(2·4)=2f(4)+4f(2)=8f(2)+4f(2)=12f(2)=24,…,f(2n)=2f(2n-1)+2n-1f(2)
=…=n·2n,故an=![]() 2n为等比数列;同理对④由于an=
2n为等比数列;同理对④由于an=![]() =n为等差数列.
=n为等差数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 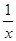 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
