题目内容
如图,矩形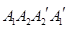 ,满足
,满足 在
在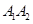 上,
上,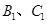 在
在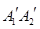 上,且
上,且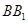 ∥
∥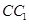 ∥
∥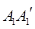 ,
,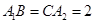 ,
,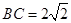 ,
,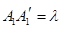 ,沿
,沿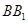 、
、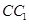 将矩形
将矩形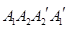 折起成为一个直三棱柱,使
折起成为一个直三棱柱,使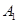 与
与 、
、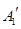 与
与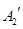 重合后分别记为
重合后分别记为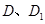 ,在直三棱柱
,在直三棱柱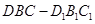 中,点
中,点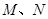 分别为
分别为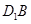 和
和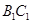 的中点.
的中点.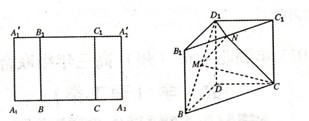
(I)证明: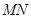 ∥平面
∥平面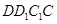 ;
;
(Ⅱ)若二面角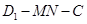 为直二面角,求
为直二面角,求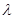 的值.
的值.
 详见解析;
详见解析;
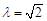 .
.
解析试题分析: 连结DB1 、DC1,由
连结DB1 、DC1,由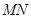 是
是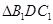 的中位线来证明线面平行.
的中位线来证明线面平行. 由条件可知∠BDC = 90°.再建系求出各点坐标,求面
由条件可知∠BDC = 90°.再建系求出各点坐标,求面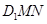 的法向量
的法向量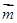 ,面
,面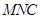 的法向量
的法向量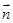 ,由二面角
,由二面角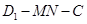 为直二面角得
为直二面角得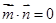 ,从而解得
,从而解得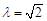 .
.
试题解析:(Ⅰ)证:连结DB1 、DC1 ∵四边形DBB1D1为矩形,M为D1B的中点 2分
∴M是DB1与D1B的交点,且M为DB1的中点
∴MN∥DC1,∴MN∥平面DD1C1C 4分
(Ⅱ)解:四边形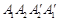 为矩形,B.C在A1A2上,B1.C1在
为矩形,B.C在A1A2上,B1.C1在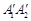 上,
上,
且BB1∥CC1∥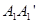 ,A1B = CA2 = 2,
,A1B = CA2 = 2,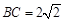 ,
,
∴∠BDC = 90° 6分
以DB、DC、DD1所在直线分别为x.y.z轴建立直角坐标系,则
D(0,0,0),B(2,0,0),C(0,2,0),D1(0,0,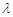 ),B1(2,0,
),B1(2,0,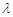 ),C1(0,2,
),C1(0,2,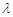 )
)
点M、N分别为D1B和B1C1的中点,∴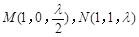
设平面D1MN的法向量为m = (x,y,z),则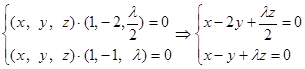 ,
,
令x = 1得: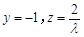
即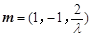 8分
8分
设平面MNC的法向量为n = (x,y,z),则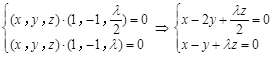 ,令z = 1得:
,令z = 1得: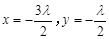
即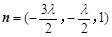 10分
10分
∵二面角D1-MN-C为直二面角 ∴m⊥n,故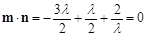 ,解得:
,解得: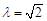
∴二面角D1-MN-C为直二面角时,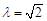 . 12分
. 12分
考点:1.点、线、面的位置关系;2.空间向量的应用;3.二面角.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案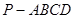 的底面
的底面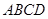 为正方形,
为正方形,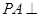 底面
底面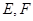 分别是
分别是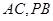 的中点.
的中点.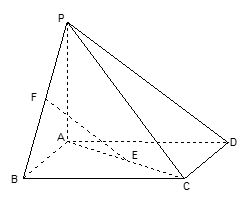
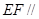 平面
平面 ;
;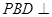 平面
平面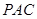 ;
;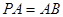 ,求
,求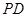 与平面
与平面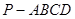 中,底面
中,底面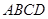 是矩形,
是矩形,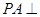 底面
底面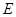 是
是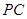 的中点,已知
的中点,已知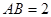 ,
,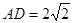 ,
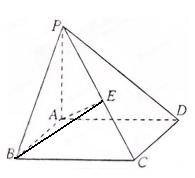
,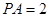 ,
,
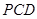 的面积;(II)三棱锥
的面积;(II)三棱锥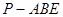 的体积
的体积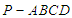 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为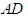 的中点。
的中点。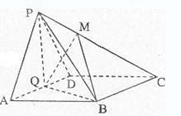
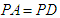 ,求证:平面
,求证:平面 ;
; 在线段
在线段 上,
上,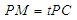 ,试确定
,试确定 的值,使
的值,使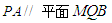 ;
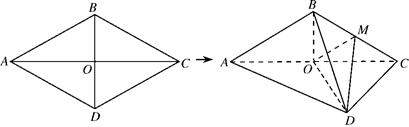
; 的边长为4,
的边长为4,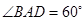 ,
,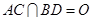 .将菱形
.将菱形 折起,得到三棱锥
折起,得到三棱锥 ,点
,点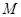 是棱
是棱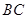 的中点,
的中点, .
.
 平面
平面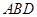 ;
;
 平面
平面 ;
; 的体积.
的体积. ,曲线
,曲线 在
在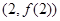 处的切线过点
处的切线过点 .
. 的解析式;
的解析式;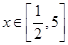 时,求
时,求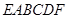 的底面
的底面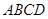 是边长为
是边长为 的正方形,
的正方形,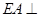 底面
底面 ,且
,且 .
. 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
 中,
中,
 为
为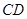 的中点,沿
的中点,沿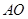 将三角形
将三角形 折起,使
折起,使 .
. ;
;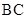 与平面
与平面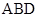 所成角的正弦值.
所成角的正弦值.
 中,
中,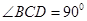 ,
, 平面
平面 ,
,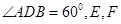 分别是直线
分别是直线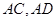 上的点,且
上的点,且

 平面角的余弦值
平面角的余弦值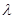 为何值时,平面
为何值时,平面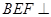 平面
平面