题目内容
已知函数 ,曲线
,曲线 在
在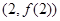 处的切线过点
处的切线过点 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)当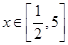 时,求
时,求 的取值范围.
的取值范围.
(Ⅰ)f(x)=lnx+ ; (Ⅱ)f(x)的取值范围是[1,ln5+
; (Ⅱ)f(x)的取值范围是[1,ln5+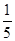 ].
].
解析试题分析:(Ⅰ)利用导数的几何含义确定曲线的切线方程的斜率,然后借助切线过点建立等量关系;(Ⅱ)根据函数的定义域,借助求导分析函数的单调性,进而确定函数的最大值和最小值.
试题解析:(Ⅰ)f¢(x)= -
- =
= .
.
则f¢(2)= ,f(2)=ln2+
,f(2)=ln2+ .
.
则曲线y=f(x)在(2,f(2))处的切线为y= (x-2)+ln2+
(x-2)+ln2+ ,
,
即y= x+m-1+ln2. 3分
x+m-1+ln2. 3分
依题意,m-1+ln2=ln2,所以m=1.
故f(x)=lnx+ . 5分
. 5分
(Ⅱ)由(Ⅰ)知,f(x)=lnx+ ,f¢(x)=
,f¢(x)= .
.
当x∈[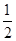 ,1]时,f¢(x)≤0,f(x)单调递减,此时,f(x)∈[1,2-ln2];
,1]时,f¢(x)≤0,f(x)单调递减,此时,f(x)∈[1,2-ln2];
当x∈[1,5]时,f¢(x)≥0,f(x)单调递增,此时,f(x)∈[1,ln5+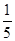 ]. 10分
]. 10分
因为(ln5+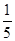 )-(2-ln2)=ln10-
)-(2-ln2)=ln10- >lne2-
>lne2- =
=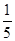 ,
,
所以ln5+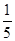 >2-ln2.
>2-ln2.
因此,f(x)的取值范围是[1,ln5+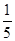 ]. 12分
]. 12分
考点:1.函数的单调性、极值和最值;2.导数的几何含义.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
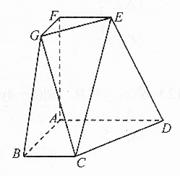
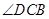 =45
=45 ,O是BC的中点,AO=
,O是BC的中点,AO=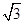 ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2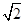 ,
,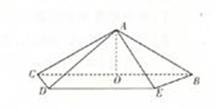
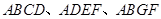 均为全等的直角梯形,且
均为全等的直角梯形,且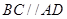 ,
,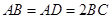 .
.
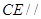 平面
平面 ;
;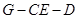 的余弦值.
的余弦值. 是边长为2的正三角形. 若
是边长为2的正三角形. 若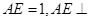 平面
平面 ,平面
,平面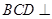 平面
平面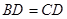 ,且
,且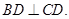
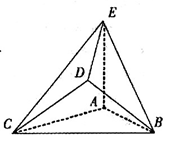
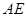 //平面
//平面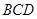 ;
; 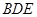
 平面
平面 .
. 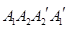 ,满足
,满足 在
在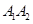 上,
上,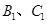 在
在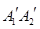 上,且
上,且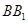 ∥
∥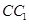 ∥
∥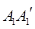 ,
,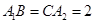 ,
,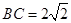 ,
,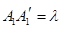 ,沿
,沿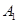 与
与 、
、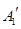 与
与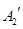 重合后分别记为
重合后分别记为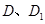 ,在直三棱柱
,在直三棱柱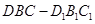 中,点
中,点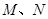 分别为
分别为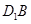 和
和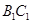 的中点.
的中点.
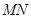 ∥平面
∥平面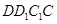 ;
;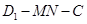 为直二面角,求
为直二面角,求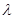 的值.
的值.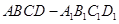 中,底面
中,底面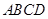 为正方形,
为正方形,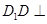 面
面 ,
,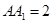 ,点
,点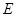 在棱
在棱 上,且
上,且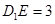 .
.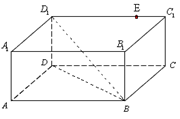
 上确定一点
上确定一点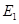 ,使得直线
,使得直线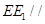 平面
平面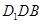 ,并证明;
,并证明; 在底面
在底面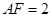 ,请说明点
,请说明点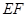 长度的最小值.
长度的最小值.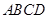 是正方形,
是正方形,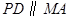 ,
,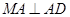 ,
, ,
, 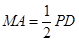 .
.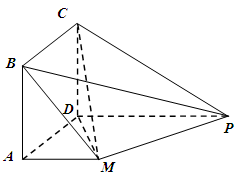
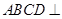 平面
平面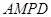 ;
;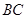 与
与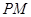 所成的角为
所成的角为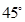 ,求二面角
,求二面角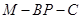 的余弦值.
的余弦值. 中,
中,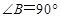 ,
,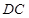 ∥
∥ ,
,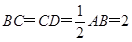 ,
, 为线段
为线段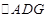 沿
沿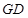 折起,使平面
折起,使平面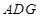 ⊥平面
⊥平面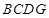 ,得到几何体
,得到几何体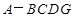 .
.
 ,
, 分别为线段
分别为线段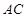 ,
,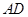 的中点,求证:
的中点,求证: ∥平面
∥平面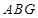 ;
;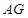 ⊥平面
⊥平面 的值.
的值.