题目内容
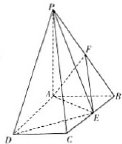 如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F中PB的中点,点E在边BC上移动.(1)证明:PE⊥AF;
(2)当点E是BC的中点时,求多面体PADEF的体积.
分析:(1)由题意可得此题是证明线面垂直的问题,即证明直线AF垂直于平面PBE,而当点E在BC上无论怎样运动时直线PE都在此平面内,因此只需证明已知直线垂直于平面内的两条相交直线即可.
(2)多面体PADEF的体积V=VP-ADE+VE-PAF,分别求出两个棱锥的底面积和高,代入棱锥体积公式,可求出答案.
(2)多面体PADEF的体积V=VP-ADE+VE-PAF,分别求出两个棱锥的底面积和高,代入棱锥体积公式,可求出答案.
解答: 证明:(1)∵PA⊥平面ABCD,BE?平面ABCD,
证明:(1)∵PA⊥平面ABCD,BE?平面ABCD,
∴EB⊥PA,
又∵EB⊥AB,AB∩AP=A,AB,AP?平面PAB,
∴EB⊥平面PAB,
又∵AF?平面PAB,
∴AF⊥BE,
又∵PA=AB=1,点F是PB的中点,
∴AF⊥平面PBE.
∵PE?平面PBE,
∴AF⊥PE.
(2)∵PD与平面ABCD所成角是30°,
∴AD=
又∵ABCD是矩形,PA=AB=1,ABCD是矩形,PA=AB=1,
∵棱锥P-ADE的高PA=1,底面ADE面积S1=
×1×
=
∴VP-ADE=
•
•1=
棱锥E-PAF的高
BC=
,底面PAF的面积S2=
×
=
∴VE-PAF=
•
•
=
∴多面体PADEF的体积V=VP-ADE+VE-PAF=
+
=
 证明:(1)∵PA⊥平面ABCD,BE?平面ABCD,
证明:(1)∵PA⊥平面ABCD,BE?平面ABCD,∴EB⊥PA,
又∵EB⊥AB,AB∩AP=A,AB,AP?平面PAB,
∴EB⊥平面PAB,
又∵AF?平面PAB,
∴AF⊥BE,
又∵PA=AB=1,点F是PB的中点,
∴AF⊥平面PBE.
∵PE?平面PBE,
∴AF⊥PE.
(2)∵PD与平面ABCD所成角是30°,
∴AD=
| 3 |
又∵ABCD是矩形,PA=AB=1,ABCD是矩形,PA=AB=1,
∵棱锥P-ADE的高PA=1,底面ADE面积S1=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴VP-ADE=
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
棱锥E-PAF的高
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴VE-PAF=
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 24 |
∴多面体PADEF的体积V=VP-ADE+VE-PAF=
| ||
| 6 |
| ||
| 24 |
5
| ||
| 24 |
点评:本题考查的知识点是空间线面垂直与线线垂直之间的转化,组合几何体的体积,其中(1)的关键是熟练掌握空间线线垂直与线面垂直的之间的相互转化,(2)的关键是将组合体时行分解.

练习册系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点. 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2, (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.