题目内容
【题目】已知二次函数f(x)=ax2+bx,(a,b为常数,且a≠0)满足条件f(2﹣x)=f(x﹣1),且方程f(x)=x有两个相等的实根.
(1)求f(x)的解析式;
(2)设g(x)=kx+1,若F(x)=g(x)﹣f(x),求F(x)在[1,2]上的最小值;
(3)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]与[2m,2n],若存在,求出m,n的值,若不存在,请说明理由.
【答案】
(1)解:由题意知f(x)=ax2+bx关于x= ![]() 对称
对称
∴﹣ ![]() =
= ![]()
ax2+bx=x有两个相等的实根,∴△=0
∴ ![]()
所以,f(x)=﹣x2+x
(2)解:F(x)=kx+1+x2﹣x=x2+(k﹣1)x+1
F(x)的对称轴为:x=﹣ ![]()
①当﹣ ![]() ≤1时, F(x)min=F(1)≤k+1
≤1时, F(x)min=F(1)≤k+1
②当 1<﹣ ![]() ≤2时,
≤2时, ![]()
③当﹣ ![]() >2 时, F(x)min=F(2)=2k+3
>2 时, F(x)min=F(2)=2k+3
∴F(x)min= 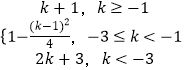
(3)解:f(x)=﹣x2+x=﹣(x﹣ ![]() )2+
)2+ ![]()
∴2n ![]() n
n ![]()
∴f(x)在[m,n]上单调递增
∴ ![]()
![]()
∵m<n
∴ ![]()
【解析】1、本题考查的是一元二次函数解析式的求法;根据对称轴,根的情况求出函数解析式里的未知数。
2、本题考查的是一元二次函数在指定区间上的最值问题,对称轴在指定的区间内就能取到最值,不在则根据单调性去求得。
3、本题考查的是一元二次函数三要素定义域、值域、对应法则以及单调性的简单应用。
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目