题目内容
(满分12分)某专卖店销售一新款服装,日销售量(单位为件)f (n) 与时间n(1≤n≤30、nÎ N*)的函数关系如下图所示,其中函数f (n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
(Ⅰ)求f (n) 的表达式,及前m天的销售总数;
(Ⅱ)按以往经验,当该专卖店销售某款服装的总数超过 400 件时,市面上会流行该款服装,而日销售量连续下降并低于 30 件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过 10 天?请说明理由.

(Ⅰ)求f (n) 的表达式,及前m天的销售总数;
(Ⅱ)按以往经验,当该专卖店销售某款服装的总数超过 400 件时,市面上会流行该款服装,而日销售量连续下降并低于 30 件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过 10 天?请说明理由.

(Ⅰ) f (n) = ,(nÎN*)
前 12 天的销售总量为 354 件
(Ⅱ) 见解析
前 12 天的销售总量为 354 件
(Ⅱ) 见解析
(I) 根据题意,设f (n) = (nÎN*), 1分
而 f (1) = 2,∴ 5 + a =" 2" Þa = -3. 2分
又 5m + a = -3m + b,∴b = 8m + a = 8m-3, 3分
∴ f (n) = (nÎN*). 4分
由 f (m) = 57得m = 12. 5分
∴ f (n) = ,(nÎN*) 6分
前 12 天的销售总量为 5 (1 + 2 + 3 + … + 12)-3×12 =" 354" 件. 7分
(II) 第 13 天的销售量为f (13) = -3×13 + 93 =" 54" 件, 8分
而 354 + 54 > 400 件,
∴ 从第 14 天开始销售总量超过 400 件,即开始流行. 9分
设第x 天的日销售量开始低于 30 件 (12 < x≤ 30),
即f (x) = -3x + 93 < 30 , 10分
解得x > 21. 11分
∴ 从第 22 天开始日销售量低于 30 件.
 ∵ 21-13 = 8,
∵ 21-13 = 8,
∴ 该服装流行的时间不超过10天. 12分
而 f (1) = 2,∴ 5 + a =" 2" Þa = -3. 2分
又 5m + a = -3m + b,∴b = 8m + a = 8m-3, 3分
∴ f (n) = (nÎN*). 4分
由 f (m) = 57得m = 12. 5分
∴ f (n) = ,(nÎN*) 6分
前 12 天的销售总量为 5 (1 + 2 + 3 + … + 12)-3×12 =" 354" 件. 7分
(II) 第 13 天的销售量为f (13) = -3×13 + 93 =" 54" 件, 8分
而 354 + 54 > 400 件,
∴ 从第 14 天开始销售总量超过 400 件,即开始流行. 9分

设第x 天的日销售量开始低于 30 件 (12 < x≤ 30),
即f (x) = -3x + 93 < 30 , 10分
解得x > 21. 11分
∴ 从第 22 天开始日销售量低于 30 件.
 ∵ 21-13 = 8,
∵ 21-13 = 8,∴ 该服装流行的时间不超过10天. 12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
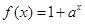
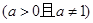 ,
,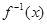 是
是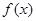 的反函数. 若
的反函数. 若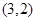 ,则
,则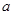 等于( )
等于( )



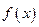 在定义域
在定义域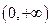 上为增函数,且满足
上为增函数,且满足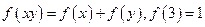
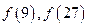 的值 (2)解不等式
的值 (2)解不等式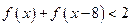

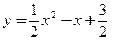 的定义域和值域都是
的定义域和值域都是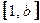 ,则实数
,则实数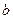 的值为 ( )
的值为 ( )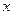 的方程
的方程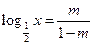 在区间(0,1)上有解,则实数m的取值范围是( )
在区间(0,1)上有解,则实数m的取值范围是( )




 ,则
,则 .
.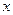 的实系数方程
的实系数方程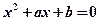 有两个根,一个根在区间
有两个根,一个根在区间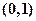 内,另一根在区间
内,另一根在区间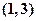 内,记点
内,记点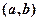 对应的区域为S.那么区域S的面积是 .
对应的区域为S.那么区域S的面积是 .