题目内容
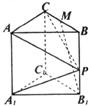 如图,正三棱柱ABC-A1B1C1的各棱长都是2,M是BC的中点,P是侧棱BB1上一点,且A1P⊥B1M.
如图,正三棱柱ABC-A1B1C1的各棱长都是2,M是BC的中点,P是侧棱BB1上一点,且A1P⊥B1M.(1)试求A1P与平面APC所成角的正弦;
(2)求点A1到平面APC的距离.
分析:(1)先建立适当的空间直角坐标系,写出相关各点的坐标,再利用垂直关系的向量表示即可求得点P的坐标;进一步求出平面APC的法向量,最后利用向量的夹角公式即可求出直线A1P与平面APC所成角;
(2)先利用空间中两点的距离公式求出:|
|=
=
,设A1到平面PAC的距离为d,最后结合d与|A1P|的关系即可求出d值.
(2)先利用空间中两点的距离公式求出:|
| A1P |
1+3+
|
| ||
| 2 |
解答: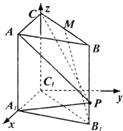 解:建立如图所示的空间直角坐标系,
解:建立如图所示的空间直角坐标系,
则相关各点的坐标为A1(2,0,0),B1(1,
,0),P(1,
,z),M(
,
,2),C(0,0,2),A(2,0,2)
由A1P⊥B1M知
•
=0
∴(-1,
,z)•(-
,-
,2)=
-
+2z=0,∴z=
,
即点P的坐标为P(1,
,
).
(1)设平面APC的法向量为n=(x,y,z),
由
即
∴n=(0,
z,z).
取z=-1,则有n=(0,-
,-1),方向指向平面APC的左下方,又
=(1,-
,-
),cos<
,n>=
=
=
.
设直线A1P与平面APC所成角为α,则sinα=
.
(2)|
|=
=
,设A1到平面PAC的距离为d,则d=|
|sinα=
•
=
=
.
 解:建立如图所示的空间直角坐标系,
解:建立如图所示的空间直角坐标系,则相关各点的坐标为A1(2,0,0),B1(1,
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
由A1P⊥B1M知
| A1P |
| B1M |
∴(-1,
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
即点P的坐标为P(1,
| 3 |
| 1 |
| 2 |
(1)设平面APC的法向量为n=(x,y,z),
由
|
|
| ||
| 2 |
取z=-1,则有n=(0,-
| ||
| 2 |
| PA1 |
| 3 |
| 1 |
| 2 |
| PA1 |
| ||
|
|
| 8 | ||||
|
8
| ||
| 119 |
设直线A1P与平面APC所成角为α,则sinα=
8
| ||
| 119 |
(2)|
| A1P |
1+3+
|
| ||
| 2 |
| A1P |
| ||
| 2 |
| 8 | ||
|
| 4 | ||
|
4
| ||
| 7 |
点评:本题主要考查了直线与平面之间所成角、点、线、面间的距离计算,考查空间想象能力、利用空间向量的运算能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.