题目内容
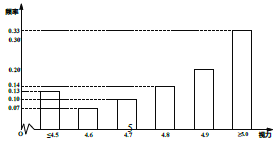
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，得到如图的频率分布直方图（图1）.
（1）若直方图中后四组的频数成等差数列，试估计全年级视力在5.0以下的人数；
（2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在1～50名和951～1000名的学生进行了调查，得到图2中数据，根据表中的数据，能否在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系？
【答案】(1)820;(2) 在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系..
【解析】【试题分析】（1）依题意设出成等差数列的的四项，利用和为
求出公差，求出每一项后可求得视力在
以下的频率，由此估计全年级视力在
以下的人数.（2）通过计算
可知在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.
【试题解析】
（Ⅰ）由图可知，第一组有3人，第二组7人，第三组27人，
设后四组的频数构成的等差数列的公差为d,
则（27-d）+(27-2d)+(27-3d)=63，解得d=3
所以后四组频数依次为
所以视力在5.0以下的频数为3+7+27+24+21=82人，
故全年级视力在5.0以下的人数约为1000×0.82＝820(人)
（Ⅱ）
因此在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.
【题目】2017年交警统计了某路段过往车辆的车速大小与发生交通事故的次数，得到如表所示的数据：
车速x（km/h） | 60 | 70 | 80 | 90 | 100 |
事故次数y | 1 | 3 | 6 | 9 | 11 |
（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，求出y关于x的线性回归方程
=
x+
；
（3）根据（2）所得速度与事故发生次数的规律，试说明交管部门可采取什么措施以减少事故的发生．
附：=
，=
-
