题目内容
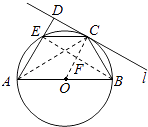
【题目】如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E. 
(1)求证:ABDE=BCCE;
(2)若AB=8,BC=4,求线段AE的长.
【答案】
(1)证明:连接BE,OC,AC,OC∩BE=F,则
∵CD是圆O的切线,
∴OC⊥l,
∵AD⊥l,∴AD∥OC,
∵AB是圆O的直径,∴AD⊥BE,
∵AD⊥l,∴l∥BE,
∴∠DCE=∠CBE=∠CAB,
∵∠EDC=∠BCA=90°,
∴△EDC∽△BCA,
∴ ![]() =
= ![]() ,
,
∴ABDE=BCCE
(2)解:由(1)可知四边形EFCD是矩形,
∴DE=CF,
∵圆O的直径AB=8,BC=4,
∴∠ABC=60°
∴△OBC是等边三角形,
∴∠EBA=30°,AE=4.
【解析】(1)连接BE,OC,OC∩BE=F,证明△EDC∽△BCA,即可证明ABDE=BCCE;(2)证明四边形EFCD是矩形,△OBC是等边三角形,即可得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某技术公司新开发了A,B两种新产品,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种产品各100件进行检测,检测结果统计如下:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
产品A | 8 | 12 | 40 | 32 | 8 |
产品B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计产品A,产品B为正品的概率;
(2)生产一件产品A,若是正品可盈利80元,次品则亏损10元;生产一件产品B,若是正品可盈利100元,次品则亏损20元;在(1)的前提下.记X为生产一件产品A和一件产品B所得的总利润,求随机变量X的分布列和数学期望.



