题目内容
【题目】已知AD与BC是四面体ABCD中相互垂直的棱,若AD=BC=6,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是( )
A.![]()
B.![]()
C.18
D.36
【答案】A
【解析】解:过C作CF⊥AD,垂足为F,连接BF,
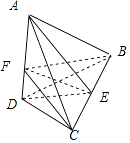
∵BC⊥AD,CF⊥AD,BC∩CF=C,
∴AD⊥平面BCF,
∴VA﹣BCD= ![]() S△BCFAD=2S△BCF.
S△BCFAD=2S△BCF.
又∠ACD=∠ABD,AD⊥平面BCF,
∴△ACD≌△ABD,∴CF=BF,
取BC的中点E,则EF⊥BC,
∴2S△ADE=2× ![]() ×BC×EF=6EF,
×BC×EF=6EF,
∴当EF最大时,棱锥的体积取得最大值.
又EF= ![]() =
= ![]() ,故当CF最大时,棱锥体积最大,
,故当CF最大时,棱锥体积最大,
∵∠ACD=60°,AD=6,∴当AC=CD时,CF取得最大值,
此时CF= ![]() =3
=3 ![]() ,∴EF=3
,∴EF=3 ![]()
∴棱锥的体积最大值为6EF=18 ![]() .
.
故选A.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
【题目】医学上所说的“三高”通常是指血脂增高、血压增高、血糖增高等疾病.为了解“三高”疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(2)能否在犯错误的概率不超过0.005的前提下认为患“三高”疾病与性别有关? 下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() .
.