题目内容

矩形ABCD中，AB=4，BC=3，沿AC将矩形ABCD折成一个30°直二面角B-AC-D，则四面体ABCD的外接球的体积为
 
．
分析：先确定球心的位置，然后求出球的半径，再解出外接球的体积．
解答：解：由题意知，球心到四个顶点的距离相等，
所以球心在对角线AC上，且其半径为AC长度的一半，
则V球=
4
3
π×（
5
2
）3=
125π
6
．
故答案为：
125π
6
点评：本题考查球的内接多面体，球的体积，考查学生发现问题解决问题的能力，是基础题．
练习册系列答案
相关题目
已知矩形ABCD中，AB=2，AD=4，动点P在以点C为圆心，1为半径的圆上，若
AP
=λ
AB
+μ
AD
（λ，μ∈R），则λ+2μ的取值范围是（　　）
在矩形ABCD中，AB=2，AD=3，如果向该矩形内随机投一点P，那么使得△ABP与△CDP的面积都不小于1的概率为
1
3
1
3
．
已知矩形ABCD中，AB=6，BC=6
2
，E为AD的中点沿BE将△ABE折起，使二面角A-BE-C为直二面角且F为AC的中点．
（1）求证：FD∥平面ABE；
（2）求二面角E-AB-C的余弦值．
如图，在矩形ABCD中，|
AB
|=4，|
BC
|=3，BE⊥AC于E，
AB
=
a
，
AD
=
b
，若以
a
、
b
为基底，则
BE
可表示为
16
25
b
-
9
25
a
16
25
b
-
9
25
a
．
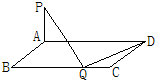精英家教网如图，矩形ABCD中，AB=1，BC=a，PA⊥平面ABCD，若在BC上只有一个点Q满足PQ⊥DQ，则a的值等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网