题目内容
【题目】某校在高二数学竞赛初赛后,对90分及以上的成绩进行统计,其频率分布直方图如图所示,若![]() 分数段的参赛学生人数为2.
分数段的参赛学生人数为2.
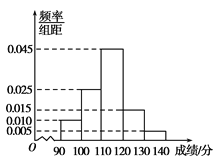
(1)求该校成绩在![]() 分数段的参赛学生人数;
分数段的参赛学生人数;
(2)估计90分及以上的学生成绩的众数、中位数和平均数(结果保留整数)
【答案】(1)![]() 人;(2)众数为115,中位数约为113,平均数约为113
人;(2)众数为115,中位数约为113,平均数约为113
【解析】
(1)首先求分数在![]() 分数段的参赛学生的频率,再求样本容量,再求成绩在
分数段的参赛学生的频率,再求样本容量,再求成绩在![]() 的频率,最后求人数;(2)众数是频率分布直方图最高的矩形所在成绩区间的中点,中位数的左右两侧的频率分别都是0.5,平均数是每一组的中间值乘以本组的频率的和,根据定义分别计算.
的频率,最后求人数;(2)众数是频率分布直方图最高的矩形所在成绩区间的中点,中位数的左右两侧的频率分别都是0.5,平均数是每一组的中间值乘以本组的频率的和,根据定义分别计算.
解:(1)由题可知:![]() 分数段的参赛学生频率为:
分数段的参赛学生频率为:
![]() ,
,
∴![]() (人).
(人).
∵成绩在![]() 分数段的参赛学生频率为:
分数段的参赛学生频率为:
![]() ,
,
∴该校成绩在![]() 分数段的参赛学生人数为:
分数段的参赛学生人数为:
![]() (人).
(人).
(2)由图可知:
90分及以上的学生成绩的众数为![]() (分).
(分).
设90分及以上的学生成绩的中位数为x.
∵![]() ,
,
∴![]() ,
,
∴90分及以上的学生成绩的中位数为113分.
90分及以上的学生成绩的平均数为:
![]()
![]()
∴90分及以上的学生成绩的众数为115,中位数约为113,平均数约为113.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关?
参考公式和数据:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |



