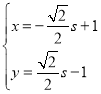题目内容
【题目】斐波那契数列0,1,1,2,3,5,8,13,…,是意大利数学家列昂纳多·斐波那契发明的,定义如下:![]() ,
,![]() ,
,![]() .某同学设计了一个求解斐波那契数列前
.某同学设计了一个求解斐波那契数列前![]() 项和的程序框图,如图所示,若输出
项和的程序框图,如图所示,若输出![]() 的值为232,则处理框和判断框中应该分别填入( )
的值为232,则处理框和判断框中应该分别填入( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
【答案】B
【解析】
模拟程序的运行,可得在每次循环中,计算出![]() 的值后,变量
的值后,变量![]() 的值变为下一个连续三项的第一项
的值变为下一个连续三项的第一项![]() ,即
,即![]() ,变量
,变量![]() 的值为下一个连续三项的第二项
的值为下一个连续三项的第二项![]() ,即
,即![]() ,从而判断矩形框应填
,从而判断矩形框应填![]() ,由
,由![]() 从
从![]() 加到
加到![]() ,判断菱形框应填
,判断菱形框应填![]() .
.
由题意知,程序框图中变量![]() 为累加变量,变量
为累加变量,变量![]() (其中
(其中![]() )为数列连续三项,在每一次循环中,计算出
)为数列连续三项,在每一次循环中,计算出![]() 的值后,变量
的值后,变量![]() 的值变为下一个连续三项的第一项
的值变为下一个连续三项的第一项![]() ,即
,即![]()
变量![]() 的值为下一个连续三项的第二项
的值为下一个连续三项的第二项![]() ,即
,即![]() ,所以矩形框应填入
,所以矩形框应填入![]()
![]()
没进入循环之前,![]() 为前两项和,则要加到
为前两项和,则要加到![]() ,还要执行循环10次,即
,还要执行循环10次,即![]() 时,循环终止,输出
时,循环终止,输出![]() ,则判断框应填入
,则判断框应填入![]()
故选:B

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
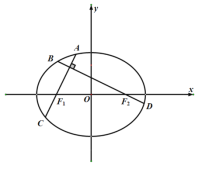
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的一个动点,且
上的一个动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() :
:![]() 于另一点
于另一点![]() .若
.若![]() 的面积为3,求直线
的面积为3,求直线![]() 的斜率.
的斜率.
【题目】下表是某城市在2019年1月份至10月份各月最低温与最高温(℃)的数据表,已知该城市的各月最低温与最高温具有相关关系,根据该表,则下列结论错误的是( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
最高温 | 5 | 9 | 9 | 11 | 17 | 24 | 27 | 30 | 31 | 21 |
最低温 |
|
| 1 |
| 7 | 17 | 19 | 23 | 25 | 10 |
A.最低温与最高温为正相关
B.每月最低温与最高温的平均值在前8个月逐月增加
C.月温差(最高温减最低温)的最大值出现在1月
D.1至4月温差(最高温减最低温)相对于7至10月,波动性更大