题目内容
给出下列命题:
①在各自的定义域上,函数y=-
,y=x
,y=(x-1)2,y=x3中有三个是增函数;
②若logm3<logn3<0,则0<n<m<1;
③若函数f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;
④已知函数f(x)=
,则函数g(x)=f(x)-
有2个零点,
其中真命题是
①在各自的定义域上,函数y=-
| 1 |
| x |
| 1 |
| 2 |
②若logm3<logn3<0,则0<n<m<1;
③若函数f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;
④已知函数f(x)=
|
| 1 |
| 2 |
其中真命题是
②③④
②③④
.分析:①根据函数单调性性质可知y=-
在定义域上不单调.②由换底公式判断.③根据奇函数的性质,利用函数图象平移判断.④作出函数图象,由图象判断.
| 1 |
| x |
解答:解:①函数y=-
在定义域上不单调.所以①错误.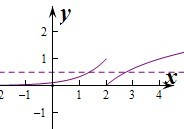
②由logm3<logn3<0得
<
<0,即log3n<log3m<0,所以0<n<m<1,所以②正确.
③函数f(x)是奇函数,则f(x)关于原点(0,0)对称,将函数f(x)向右平移一个单位得到f(x-1),此时函数f(x-1)的图象关于点A(1,0)对称,所以③正确.
④作出函数f(x)的图象由图象可知函数g(x)=f(x)-
有2个零点.正确.
故答案为:②③④
| 1 |
| x |

②由logm3<logn3<0得
| 1 |
| log?3m |
| 1 |
| log?3n |
③函数f(x)是奇函数,则f(x)关于原点(0,0)对称,将函数f(x)向右平移一个单位得到f(x-1),此时函数f(x-1)的图象关于点A(1,0)对称,所以③正确.
④作出函数f(x)的图象由图象可知函数g(x)=f(x)-
| 1 |
| 2 |
故答案为:②③④
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
相关题目
 则
则
 在平面
在平面 内,并且对空间任一点
内,并且对空间任一点 ,
, ,则
,则 的值为1;
的值为1;
 中,若
中,若 ,
, ,则点
,则点 到平面
到平面 的距离为
的距离为 ,其中正确命题的序号是
,其中正确命题的序号是