题目内容
给出下列命题:①有一条侧棱与底面两边垂直的棱柱是直棱柱;②底面为正多边形的棱柱为正棱柱;③顶点在底面上的射影到底面各顶点的距离相等的棱维是正棱锥;④A、B为球面上相异的两点,则通过A、B的大圆有且只有一个.其中正确命题的个数是 ( )
分析:根据直棱柱的定义可以判断①的真假;根据正棱柱的定义可以判断②的真假;根据正棱锥的定义,可以判断出③的真假;根据球的几何特征,可以判断④的真假;
解答:解:若侧棱与底面两条平行的两边垂直,则侧棱与底面不一定垂直,此时的棱柱不一定是直棱柱,故①错误;
底面为正多边形的直棱柱为正棱柱,故②错误;
顶点在底面上的射影到底面各顶点的距离相等的棱维,表示顶点在底面的射影落在底面的外心上,不一定是正棱锥,故③错误;
当A,B为球的两极点时,通过A、B的大圆有无数个,故④错误
故选A
底面为正多边形的直棱柱为正棱柱,故②错误;
顶点在底面上的射影到底面各顶点的距离相等的棱维,表示顶点在底面的射影落在底面的外心上,不一定是正棱锥,故③错误;
当A,B为球的两极点时,通过A、B的大圆有无数个,故④错误
故选A
点评:本题考查正棱锥的定义、棱锥的结构特征等基础知识,考查空间想象力.属于基础题.

练习册系列答案
相关题目












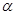 和
和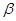 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: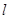 与
与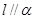 ;
; ;
;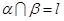 ,若
,若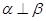 ;
;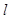 与平面
与平面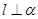 .
.