题目内容
[2013·吉林调研]已知定义在R上的函数f(x)满足f(x)＋f(－x)＝0，且在(－∞，0)上单调递增，如果x1＋x2＜0且x1x2＜0，则f(x1)＋f(x2)的值( )
| A．可能为0 | B．恒大于0 |
| C．恒小于0 | D．可正可负 |
C
由x1x2＜0不妨设x1＜0，x2＞0.
∵x1＋x2＜0，∴x1＜－x2＜0.
由f(x)＋f(－x)＝0知f(x)为奇函数．
又由f(x)在(－∞，0)上单调递增得，f(x1)＜f(－x2)＝－f(x2)，
所以f(x1)＋f(x2)＜0.故选C.
∵x1＋x2＜0，∴x1＜－x2＜0.
由f(x)＋f(－x)＝0知f(x)为奇函数．
又由f(x)在(－∞，0)上单调递增得，f(x1)＜f(－x2)＝－f(x2)，
所以f(x1)＋f(x2)＜0.故选C.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
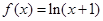
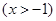
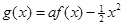
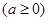的单调性。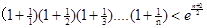
＋
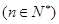
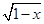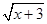的最大值为M，最小值为m，则
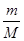的值为( )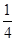
．
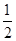
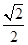
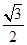
的奇偶性；
上为减函数，求
的取值范围．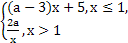
是(-∞,+∞)上的减函数,则a的取值范围是
，g(x)＝x2f(x－1)，则函数g(x)的递减区间是________．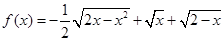
的最大值为 .