题目内容
【题目】已知几何体ABCDEF中,AB∥CD,AD⊥DC,EA⊥平面ABCD,FC∥EA,AB=AD=EA=1,CD=CF=2. 
(Ⅰ)求证:平面EBD⊥平面BCF;
(Ⅱ)求点B到平面ECD的距离.
【答案】解:(I)证明:∵AB∥CD,AD⊥DC,AB=AD=1,CD=2,
∴BD=BC= ![]() ,
,
∴BD2+BC2=CD2,
∴BD⊥BC,
∵EA⊥平面ABCD,BD平面ABCD,
∴EA⊥BD,∵EA∥FC,
∴FC⊥BD,
又BC平面BCF,FC平面BCF,BC∩CF=C,
∴BD⊥平面FBC,
又BD平面BDE,
∴平面BDE⊥平面BCF.
(II)解:过A作AM⊥DE,垂足为M,
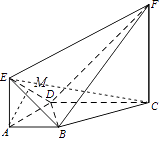
∵EA⊥平面ABCD,CD平面ABCD,
∴EA⊥CD,又CD⊥AD,EA∩AD=A,
∴CD⊥平面EAD,又AM平面EAD,
∴AM⊥CD,又AM⊥DE,DE∩CD=D,
∴AM⊥平面CDE,
∵AD=AE=1,EA⊥AD,
∴AM= ![]() ,即A到平面CDE的距离为
,即A到平面CDE的距离为 ![]() ,
,
∵AB∥CD,CD平面CDE,AB平面CDE,
∴AB∥平面CDE,
∴B到平面CDE的距离为 ![]() .
.
【解析】(I)先计算BD,BC,利用勾股定理的逆定理证明BD⊥BC,再利用EA⊥平面ABCD得出AE⊥BD,从而有CF⊥BD,故而推出BD⊥平面FBC,于是平面EBD⊥平面BCF;(II)证明AB∥平面CDE,于是B到平面CDE的距离等于A到平面CDE的距离,过A作AM⊥DE,证明AM⊥平面CDE,于是AM的长即为B到平面CDE的距离.
【考点精析】掌握平面与平面垂直的判定是解答本题的根本,需要知道一个平面过另一个平面的垂线,则这两个平面垂直.

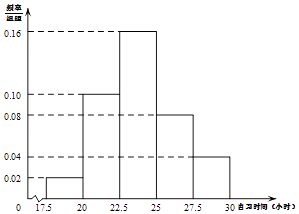
【题目】共享单车进驻城市,绿色出行引领时尚,某市有统计数据显示,2016年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示,若将共享单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”,已知在“经常使用单车用户”中有 ![]() 是“年轻人”.
是“年轻人”. 
(Ⅰ)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列2×2列联表,并根据列联表的独立性检验,判断能有多大把握可以认为经常使用共享单车与年龄有关?
使用共享单车情况与年龄列联表
年轻人 | 非年轻人 | 合计 | |
经常使用共享单车用户 | 120 | ||
不常使用共享单车用户 | 80 | ||
合计 | 160 | 40 | 200 |
(Ⅱ)将频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量X,求X的分布列与期望.
(参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中,K2= ![]() ,n=a+b+c+d)
,n=a+b+c+d)