题目内容
10.已知关于x的方程x2+2ax+b=0有两个实根x1,x2,且x1∈[-1,0],x2∈[1,2].(1)求a+b的取值范围;
(2)当a+b最小时,不等式x2+2amx+b≥mx2+m在x>-3时恒成立,求m的取值范围.
分析 (1)构造函数,建立不等式组,可得平面区域,即可求a+b的取值范围;
(2)不等式x2+2amx+b≥mx2+m在x>-3时恒成立,等价于不等式(m-1)x2+mx+m+2≥0在x>-3时恒成立.构造函数,分类讨论,即可求m的取值范围.
解答 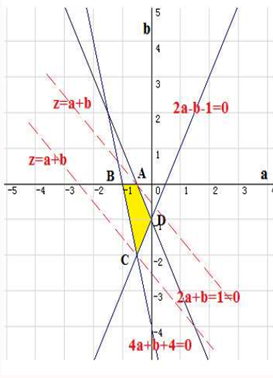 解:(1)设f(x)=x2+2ax+b,
解:(1)设f(x)=x2+2ax+b,
∵关于x的方程x2+2ax+b=0有两个实根x1,x2,且x1∈[-1,0],x2∈[1,2].
∴$\left\{\begin{array}{l}{f(-1)=1-2a+b≥0}\\{f(0)=b≤0}\\{f(1)=2a+b+1≤0}\\{f(2)=4a+b+4≥0}\end{array}\right.$,
不等式表示的区域,如图所示,
令z=a+b,则直线z=a+b过A(-$\frac{1}{2}$,0)时,z的最大值为$\frac{1}{2}$;直线z=a+b过C(-$\frac{1}{2}$,-2)时,z的最大值为-$\frac{5}{2}$.
∴a+b的取值范围是[-$\frac{5}{2}$.-$\frac{1}{2}$];
(2)由(1)知,a=-$\frac{1}{2}$,b=-2时,z=a+b最小,
∴不等式x2+2amx+b≥mx2+m在x>-3时恒成立,等价于不等式(m-1)x2+mx+m+2≥0在x>-3时恒成立.
令g(x)=(m-1)x2+mx+m+2,则
m-1=0,即m=1时,f(x)=x+3≥0在x>-3上恒成立,符合题意;
m-1≠0,即m≠1时,f(x)的对称轴x=-$\frac{m}{2(m-1)}$,则$\left\{\begin{array}{l}{m-1>0}\\{-\frac{m}{2(m-1)}≥-3}\\{△={m}^{2}-4(m-1)(m+2)≤0}\end{array}\right.$或$\left\{\begin{array}{l}{m-1>0}\\{-\frac{m}{2(m-2)}<-3}\\{f(-3)=7m-7≥0}\end{array}\right.$,
∴m≥$\frac{6}{5}$或1<m<$\frac{6}{5}$,
∴m≥1.
点评 本题考查方程根的讨论,考查线性规划知识,考查恒成立问题,考查学生分析解决问题的能力,属于难题.

| A. | 平面直角坐标系内的任意一条直线都有倾斜角和斜率 | |
| B. | 直线倾斜角的范围是0°≤α<180° | |
| C. | 若一条直线的倾斜角为α(α≠90°),则此直线的斜率为tanα | |
| D. | 与坐标轴垂直的直线的倾斜角是0°或90° |