题目内容
已知实数x,y满足关系:x2+y2-2x+4y-20=0,则x2+y2的最小值______.
把圆的方程化为标准方程得:
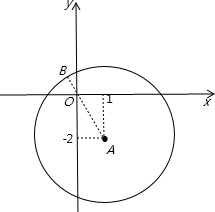
(x-1)2+(y+2)2=25,则圆心A坐标为(1,-2),圆的半径r=5,
设圆上一点的坐标为(x,y),原点O坐标为(0,0),
则|AO|=
,|AB|=r=5,
所以|BO|=|AB|-|OA|=5-
.
则x2+y2的最小值为(5-
)2=30-10
.
故答案为:30-10
(x-1)2+(y+2)2=25,则圆心A坐标为(1,-2),圆的半径r=5,
设圆上一点的坐标为(x,y),原点O坐标为(0,0),
则|AO|=
| 5 |
所以|BO|=|AB|-|OA|=5-
| 5 |
则x2+y2的最小值为(5-
| 5 |
| 5 |
故答案为:30-10
| 5 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
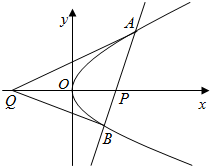
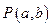 在直线
在直线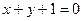 上,求
上,求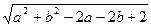 的最小值。
的最小值。