题目内容
求圆心在直线x-y-4=0上,并且经过圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0的交点的圆的方程.
设所求圆的方程为x2+y2+2x+8y-8+λ(x2+y2-4x-4y-2)=0,
整理得(1+λ)x2+(1+λ)y2+(2-4λ)x+(8-4λ)y-8-2λ=0,
∴圆心坐标为(
,
),
∵圆心在直线x-y-4=0上,
∴
-
-4=0,解得:λ=-
,
∴所求的圆的方程为x2+y2+4x+12y-10=0.
整理得(1+λ)x2+(1+λ)y2+(2-4λ)x+(8-4λ)y-8-2λ=0,
∴圆心坐标为(
| 2λ-1 |
| 1+λ |
| 2λ-4 |
| 1+λ |
∵圆心在直线x-y-4=0上,
∴
| 2λ-1 |
| 1+λ |
| 2λ-4 |
| 1+λ |
| 1 |
| 4 |
∴所求的圆的方程为x2+y2+4x+12y-10=0.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
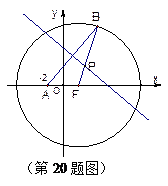
 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.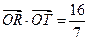 (O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(O为原点).若存在,求直线l的方程;若不存在,请说明理由.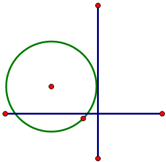
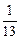 C.|a|<
C.|a|<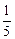 D.|a|<
D.|a|<