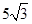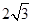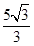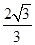题目内容
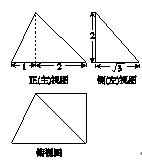
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
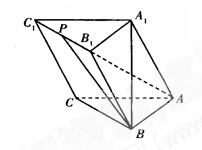
(1)求证:AC⊥BB1;
(2)若P是棱B1C1的中点,求平面PAB将三棱柱分成的两部分体积之比.

(1)求证:AC⊥BB1;
(2)若P是棱B1C1的中点,求平面PAB将三棱柱分成的两部分体积之比.
(1)详见解析; (2) .
.
 .
.试题分析:(1)要证
 ,可转化为去证明
,可转化为去证明 垂直于含有
垂直于含有 的平面
的平面 ,再由题中所给线面垂直
,再由题中所给线面垂直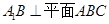 ,结合面面垂直的判定定理,可以判断得出
,结合面面垂直的判定定理,可以判断得出 ,最后结合面面垂直的性质定理,由题中所给线线垂直
,最后结合面面垂直的性质定理,由题中所给线线垂直 ,可以得到
,可以得到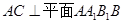 ,进而不难证得
,进而不难证得 ;(2)根据题意过
;(2)根据题意过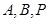 三点的平面与原三棱柱的截面是一个四边形,由
三点的平面与原三棱柱的截面是一个四边形,由 可
可得截面是一个梯形,又由
 是
是 的中点可得
的中点可得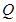 也是
也是 的中点,这样可得出两部分当中下方是一个棱台,结合棱台的体积公式不难得出它的体积,最后由已知总体积可求出另一部分的体积,进而求出体积之比.
的中点,这样可得出两部分当中下方是一个棱台,结合棱台的体积公式不难得出它的体积,最后由已知总体积可求出另一部分的体积,进而求出体积之比.试题解析:(1)在三棱柱
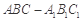 中,因为
中,因为 ,
, 平面
平面 ,所以平面
,所以平面 平面
平面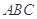 ,因为平面
,因为平面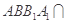 平面
平面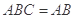 ,
, ,所以
,所以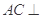 平面
平面 ,所以
,所以 .
.(2)设平面
 与棱
与棱 交于
交于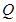 ,因为
,因为 为棱
为棱 的中点,所以
的中点,所以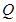 是棱
是棱 的中点,连接
的中点,连接 ,设三棱柱
,设三棱柱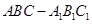 的底面积为
的底面积为 ,高为
,高为 ,体积为
,体积为 ,则
,则 ,
,

练习册系列答案
相关题目
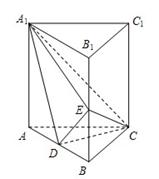
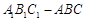 中,侧面
中,侧面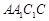
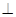 底面ABC,底面ABC是边长为2的等边三角形,侧面
底面ABC,底面ABC是边长为2的等边三角形,侧面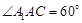 ,E、F分别是
,E、F分别是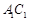 、AB的中点.
、AB的中点.
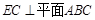 ;
;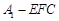 的体积.
的体积. 中,
中, 分别是
分别是 的中点,
的中点,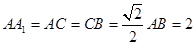 .
.
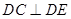 ;
;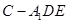 的体积.
的体积.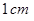 的正方形绕其一条边所在直线旋转一周,则所形成圆柱的体积等于
的正方形绕其一条边所在直线旋转一周,则所形成圆柱的体积等于 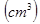 .
.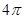 ,底面积为
,底面积为 ,则该圆锥的母线长为 .
,则该圆锥的母线长为 .