Question

【题目】如图，四棱锥P﹣ABCD中，AD⊥平面PAB，AP⊥AB．
（1）求证：CD⊥AP；
（2）若CD⊥PD，求证：CD∥平面PAB．

Answer 1

【答案】
（1）证明：因为AD⊥平面PAB，AP平面PAB，所以AD⊥AP．

又因为AP⊥AB，AB∩AD=A，AB平面ABCD，AD平面ABCD，

所以AP⊥平面ABCD．

因为CD平面ABCD，所以CD⊥AP

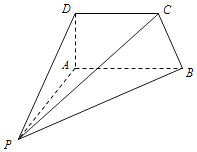
（2）证明：因为CD⊥AP，CD⊥PD，且PD∩AP=P，PD平面PAD，AP平面PAD，

所以CD⊥平面PAD．①

因为AD⊥平面PAB，AB平面PAB，所以AB⊥AD．

又因为AP⊥AB，AP∩AD=A，AP平面PAD，AD平面PAD，

所以AB⊥平面PAD．②

由①②得CD∥AB，

因为CD平面PAB，AB平面PAB，所以CD∥平面PAB

【解析】（1）推导出AD⊥AP，AP⊥AB，从而AP⊥平面ABCD，由此能证明CD⊥AP．（2）由CD⊥AP，CD⊥PD，得CD⊥平面PAD．再推导出AB⊥AD，AP⊥AB，从而AB⊥平面PAD，进而CD∥AB，由此能证明CD∥平面PAB．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．