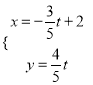题目内容
【题目】已知函数f（x）= 
，若函数g（x）=f2（x）﹣axf（x）恰有6个零点，则a的取值范围是（ ）
A.（0，3）
B.（1，3）
C.（2，3）
D.（0，2）
【答案】C
【解析】解：令g（x）=f2（x）﹣axf（x）=0，
则f（x）=0，或f（x）﹣ax=0，
①当f（x）=0时，即3x+1=0或x2﹣4x+1=0，
解得x=﹣ 
，x=2﹣ 
，x=2+ ，即有三个零点，
②当f（x）﹣ax=0，即f（x）=ax，
∵x=0时，f（0）=1≠0，即x≠0，
∴方程 
=a有三个根，
当x＜0时， =3+ 
，
当x＞0时， =|x+ ﹣4|，
分别画出y= （紫线）与y=a的图象，如右图所示，
由图可知，当a∈（2，3）时，两函数图象有三个交点，
综合以上讨论得，当a∈（2，3）时，原函数g（x）有六个零点．
所以答案是：C．
【题目】（本题满分10分）已知等差数列{an}满足a1＋a2＝10，a4－a3＝2.
(1)求{an}的通项公式．
(2)设等比数列{bn}满足b2＝a3，b3＝a7.问：b6与数列{an}的第几项相等？
【题目】某工厂生产甲，乙两种芯片，其质量按测试指标划分为：指标大于或等于82为合格品，小于82为次品．现随机抽取这两种芯片各100件进行检测，检测结果统计如下：
测试指标 | [70，76） | [76，82） | [82，88） | [88，94） | [94，100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
（1）试分别估计芯片甲，芯片乙为合格品的概率；
（2）生产一件芯片甲，若是合格品可盈利40元，若是次品则亏损5元；生产一件芯片乙，若是合格品可盈利50元，若是次品则亏损10元．在（1）的前提下，记X为生产1件芯片甲和1件芯片乙所得的总利润，求随机变量X的分布列及生产1件芯片甲和1件芯片乙所得总利润的平均值．
