题目内容
1.设m>1,在约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$下,目标函数z=x+my的最大值等于2,则m=$1+\sqrt{2}$.分析 根据m>1,可以判断直线y=mx的倾斜角位于区间($\frac{π}{4},\frac{π}{2}$)上,由此判断出满足约束条件件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$的平面区域的形状,再根据目标函数z=x+my对应的直线与直线y=mx垂直,且在直线y=mx与直线x+y=1交点处取得最大值,由此可得关于m的方程,从而求得m值.
解答 解:∵m>1,由约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$作出可行域如图,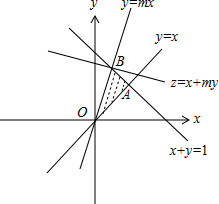
直线y=mx与直线x+y=1交于($\frac{1}{m+1},\frac{m}{m+1}$),
目标函数z=x+my对应的直线与直线y=mx垂直,且在($\frac{1}{m+1},\frac{m}{m+1}$)处取得最大值,
由题意可知$\frac{1+{m}^{2}}{m+1}=2$,又∵m>1,解得m=1+$\sqrt{2}$.
故答案为:1+$\sqrt{2}$.
点评 本题考查的知识点是简单线性规划的应用,其中根据平面直线方程判断出目标函数z=x+my对应的直线与直线y=mx垂直,且在($\frac{1}{m+1},\frac{m}{m+1}$)点取得最大值,并由此列出关于m的方程是解答本题的关键,是中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
10.为了了解潮州市居民月用电情况,抽查了该市100户居民月用电量(单位:度),得到频率分布直方图如下:根据下图可得这100户居民月用电量在〔150,300〕的用户数是( )

| A. | 70 | B. | 64 | C. | 48 | D. | 30 |
7.图中的三个直角三角形是一个体积为30cm3的几何体的三视图,则侧视图中的h为( )


| A. | 5 cm | B. | 6 cm | C. | 7 cm | D. | 8 cm |
14.一个四棱锥的三视图如图所示,那么这个四棱锥的表面积是( )
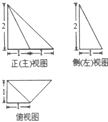

| A. | $\frac{{9+2\sqrt{3}+\sqrt{5}}}{2}$ | B. | $\frac{{9+2\sqrt{3}}}{2}$ | C. | $\frac{{9+2\sqrt{5}}}{2}$ | D. | $\frac{{11+\sqrt{5}}}{2}$ |
10.${(x-\sqrt{3}y)^8}$的展开式中x6y2项的系数是( )
| A. | 28 | B. | 84 | C. | -28 | D. | -84 |
11.已知U=R,A={x|x2≤1},B={x|y=lnx},则∁U(A∪B)=( )
| A. | (-∞,0)(1,+∞) | B. | (-∞,0)(1,+∞) | C. | (-∞,-1) | D. | (-∞,-1] |