题目内容
7．图中的三个直角三角形是一个体积为30cm3的几何体的三视图，则侧视图中的h为（ ）
| A． | 5 cm | B． | 6 cm | C． | 7 cm | D． | 8 cm |
分析 首先根据三视图把立体图整理出来进一步利用几何体的体积公式求出结果．
解答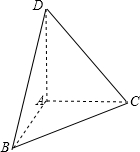 
解：根据三视图得知：
该几何体是一个三棱锥，且AB=6cm，AC=5cm，AD是三棱锥的高．
所以：$V=\frac{1}{3}×\frac{1}{2}×6×5×h=30$
解得：h=6cm．
故选：B
点评 本题考查的知识要点：三视图与立体图之间的相互转化，三棱锥体积公式的应用．主要考查学生的空间想象能力．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
17．微信是现代生活进行信息交流的重要工具，对某城市年龄在20岁至60岁的微信用户进行有关调查发现，有$\frac{1}{3}$的用户平均每天使用微信时间不超过1小时，其他人都在1小时以上；若将这些微信用户按年龄分成青年人（20岁至40岁）和中年人（40岁至60岁）两个阶段，那么其中$\frac{3}{4}$是青年人；若规定：平均每天使用微信时间在1小时以上为经常使用微信，经常使用微信的用户中有$\frac{2}{3}$是青年人．
（I）现对该市微信用户进行“经常使用微信与年龄关系”的调查，采用随机抽样的方法选取容 量为l80的一个样本，假设该样本有关数据与调查结果完全相同，列出2×2列联表．
（Ⅱ）由列表中的数据，是否有99.9%的把握认为“经常使用微信与年龄有关”？
（Ⅲ）从该城市微信用户中任取3人，其中经常使用微信的中年人人数为X，求出X的期望．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
（I）现对该市微信用户进行“经常使用微信与年龄关系”的调查，采用随机抽样的方法选取容 量为l80的一个样本，假设该样本有关数据与调查结果完全相同，列出2×2列联表．
| 青年人 | 中年人 | 合计 | |
| 经常使用微信 | |||
| 不经常使用微信 | |||
| 合计 |
（Ⅲ）从该城市微信用户中任取3人，其中经常使用微信的中年人人数为X，求出X的期望．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
18．已知双曲线M：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1（a＞0，b＞0）$两个焦点为分别为${F_1}（-\sqrt{3}，0），{F_2}（\sqrt{3}，0）$，过点F2的直线l与该双曲线的右支交于M、N两点，且△F1MN是等边三角形，则以点F2为圆心，与双曲线M的渐近线相切的圆的方程为（ ）
| A． | ${（x-\sqrt{3}）^2}+{y^2}=2$ | B． | ${（x-\sqrt{3}）^2}+{y^2}=4$ | C． | ${（x-\sqrt{3}）^2}+{y^2}=1$ | D． | ${（x-\sqrt{3}）^2}+{y^2}=\frac{3}{5}$ |
15．以坐标轴为对称轴，以原点为顶点且过圆（x-1）2+（y+3）2=1的圆心的抛物线的方程是（ ）
| A． | y=3x2或y=-3x2 | B． | y=3x2 | C． | y2=-9x或y=3x2 | D． | y=-3x2或y2=9x |
12．
某校为了调查“学业水平考试”学生的数学成绩，随机地抽取该校甲、乙两班各10名同学，获得的数据如下：（单位：分）
甲：132，108，112，121，113，121，118，127，118，129；
乙：133，107，120，113，121，116，126，109，129，127．
（1）以百位和十位为茎，个位为叶，在图5中作出以上抽取的甲、乙两班学生数学成绩的茎叶图，求出这20个数据的众数，并判断哪个班的平均水平较高；
（2）将这20名同学的成绩按下表分组，现从第一、二、三组中，采用分层抽样的方法抽取6名同学成绩作进一步的分析，求应从这三组中各抽取的人数．
某校为了调查“学业水平考试”学生的数学成绩，随机地抽取该校甲、乙两班各10名同学，获得的数据如下：（单位：分）甲：132，108，112，121，113，121，118，127，118，129；
乙：133，107，120，113，121，116，126，109，129，127．
（1）以百位和十位为茎，个位为叶，在图5中作出以上抽取的甲、乙两班学生数学成绩的茎叶图，求出这20个数据的众数，并判断哪个班的平均水平较高；
（2）将这20名同学的成绩按下表分组，现从第一、二、三组中，采用分层抽样的方法抽取6名同学成绩作进一步的分析，求应从这三组中各抽取的人数．
| 组别 | 第一 | 第二 | 第三 | 第四 |
| 分值区间 | [100，110） | [110，120） | [120，130） | [130，140] |
18．已知函数f（x）=|x-a|-|x-4a|（a＞0），若对?x∈R，都有f（2x）-1≤f（x），则实数a的最大值为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | 1 |