题目内容
8.用一块矩形铁皮作圆台形铁桶的侧面,要求铁桶的上底半径是24cm,下底半径为16cm,母线长为48cm.(1)求矩形铁皮上边的最小值;
(2)求该铁桶的容积.
分析 (1)设圆台的侧面展开图的圆心角∠AOA′=α,OA=x,根据相似三角形的性质,求出α,x的值,可得答案;
(2)根据已知求出圆台的高,代入圆台体积公式,可得答案.
解答 解:(1)如图,设圆台的侧面展开图的圆心角∠AOA′=α,OA=x,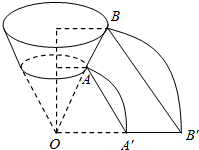
由三角形相似可得$\frac{x}{x+48}$=$\frac{16}{24}$,
解得x=96 cm.
则$\frac{2π×24}{2π(96+48)}$=$\frac{α}{360°}$,
解得α=60°,
所以△BOB′为正三角形,那么BB′=OB=96+48=144 cm.
由下图可知,矩形铁皮长边的最小值为144 cm.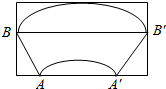
(2)∵圆台的上底半径是24cm,下底半径为16cm,母线长为48cm.
∴圆台的高h=$\sqrt{{48}^{2}-(24-16)^{2}}$=8$\sqrt{35}$cm,
故圆台的体积V=$\frac{1}{3}π$(242+162+24×16)×8$\sqrt{35}$=$\frac{9728}{3}\sqrt{35}$πcm3,
即该铁桶的容积为$\frac{9728}{3}\sqrt{35}$πcm3.
点评 本题考查的知识点是旋转体,熟练掌握圆台的展开图及相应的体积表面积公式,是解答的关键.

练习册系列答案
相关题目
16.函数f(x)=log2(4+3x-x2)的单调递减区间是( )
| A. | (-∞,$\frac{3}{2}$] | B. | [$\frac{3}{2}$,+∞) | C. | (-1,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,4) |
3.某学校有老师200人,男学生1200人,女学生1000人,现用分层抽样的方法从全体师生中抽取一个容量为n的样本,已知女学生一共抽取了80人,则n的值是( )
| A. | 193 | B. | 192 | C. | 191 | D. | 190 |
18.设函数f(x)=$\left\{\begin{array}{l}{2-x,0≤x≤1}\\{(x-2)^{2},1<x≤2}\end{array}\right.$,则f[f($\frac{3}{2}$)]的值等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{9}{4}$ |
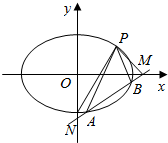 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{3}}}{2}$,过椭圆C上一点P(2,1)作倾斜角互补的两条直线,分别与椭圆交于点A、B,直线AB与x轴交于点M,与y轴负半轴交于点N.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{3}}}{2}$,过椭圆C上一点P(2,1)作倾斜角互补的两条直线,分别与椭圆交于点A、B,直线AB与x轴交于点M,与y轴负半轴交于点N.